Frequenzmodulation

Neben der älteren Amplitudenmodulation hat in der Nachrichtentechnik als weitere analoge Modulationsart die Frequenzmodulation FM einen hohen Stellenwert. Die Information, das Modulationssignal, wirkt hierbei auf die Frequenz des Trägersignals ein und lässt dessen Amplitude unverändert. Die FM gehört zur Winkelmodulation und steht in enger Beziehung zur Phasenmodulation. Der wohl bekannteste Einsatzbereich für FM ist der UKW-Rundfunkempfang und in der Veranstaltungstechnik sind es drahtlose Funkmikrofone.

• FM-Modulationssignal
• Fourierspektrum einer FM
• Besselfunktionen und FM-Spektrum
• Mathematischer Hintergrund zur FM

Beeinflusst das Informationssignal Baugruppen, die im Trägeroszillator die Frequenz bestimmen, so erhält man ein einfaches Verfahren zur Erzeugung einer FM. Handelt es sich um einen Parallelschwingkreis eines LC-Oszillators, so kann die Kapazität durch eine Kapazitätsdiode (Varicap) oder ein Kondensatormikrofon ergänzt werden. Weitere Möglichkeiten ergeben sich mit spannungsgesteuerten Sägezahn- oder Rechteckgeneratoren, die mit speziellen Diodenschaltungen ein synthetisches Sinussignal erzeugen.

Bei einem Kondensatormikrofon verändert der Schalldruck den Abstand der Membranen in der Kapsel und entsprechend variiert der Kapazitätswert. Bei der Modulation am pn-Übergang einer Kapazitätsdiode wird mit einer DC-Vorspannung eine Sperrzone aufrecht erhalten. Sie hat aufgrund ihrer Ladungsverteilung nutzbare kapazitive Eigenschaften. Eine an diese Diode zusätzlich angelegte Information, das eigentliche Modulationssignal, verändert die Sperrschichtbreite, ohne sie ganz abzubauen. Die Änderung des Kapazitätswerts und proportional dazu die Trägerfrequenz werden direkt vom Informationssignal bestimmt.

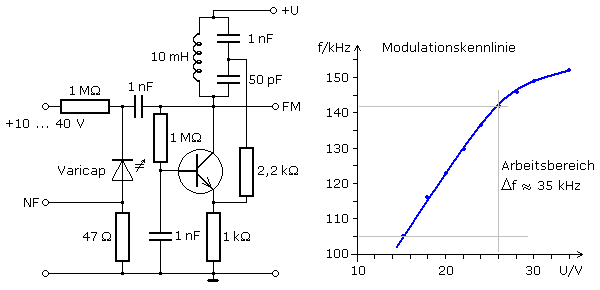
Das Bild zeigt eine Oszillatorschaltung, die zusammen mit der Varicap als FM-Modulator arbeitet. Es liegt eine Basisgrundschaltung vor, da die Basis über den 1 nF Kondensator für das Signal direkten Massebezug hat. Der LC-Generator entspricht einer Colpittsschaltung mit unterteiltem C und dem Mitkopplungszweig über 2,2 kΩ zum Emitter. Ruft man sich die Wechselstromersatzschaltung in Erinnnerung, so sind auf das Signal bezogen die Potenziale der Betriebsspannung und Masse identisch. Die Kapazitätsdiode ist folglich parallel zum LC-Schwingkreis geschaltet und ist mitbestimmend für die Frequenz des Oszillators.

Das Diagramm stellt die Modulationskennlinie dar, die ohne NF-Signal durch Verändern der Diodensperrspannung aufgenommen wurde. Der lineare Arbeitsbereich zwischen 15 und 26 V, der zur Modulation verwendet werden kann, entspricht einem Frequenzumfang von 35 kHz.

Das FM-Modulationssignal

Bei einer Diodensperrspannung von 21 V beträgt für die oben gezeigte Schaltung die Oszillator- oder Trägerfrequenz rund 125 kHz. Soll der gesamte lineare Kennlinienbereich ausgenutzt werden, kann die Amplitude des zu modulierenden NF-Signals maximal 5 V betragen. Beim positiven Spitzenwert bleibt eine Diodensperrspannung von 16 V und für den negativen Spitzenwert ergeben sich 26 V. Die beiden zugehörigen Hubfrequenzen von 108 kHz und 142 kHz sind aus dem Kennlinienverlauf ablesbar.

Es ist ein direkter Zusammenhang zwischen der NF-Amplitude und dem Frequenzhub zu erkennen. Bei der Modulation von Audiosignalen bestimmt die Lautstärke den Frequenzhub. Die folgende Grafik zeigt diese Zusammenhänge für eine große und kleine NF-Signalamplitude. Im FM-Modulationssignal werden kontinuierlich alle Frequenzen zwischen den beiden Grenzwerten durchlaufen. Im NF-Nulldurchgang tritt die unmodulierte Trägerfrequenz auf.

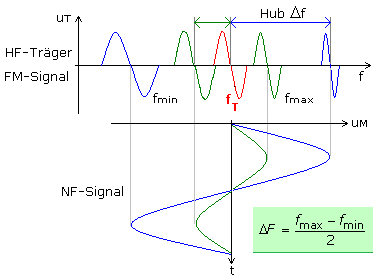
Für die folgenden Oszillogrammbilder wurden nicht realistische Frequenzverhältnisse zwischen HF und NF gewählt, um zu zeigen, wie sich eine Amplituden- oder Frequenzänderung des NF-Signals im FM-Signal darstellt. Die Trägerfrequenz ist konstant. Der Modulationsindex η verhält sich proportional zur Signalamplitude.

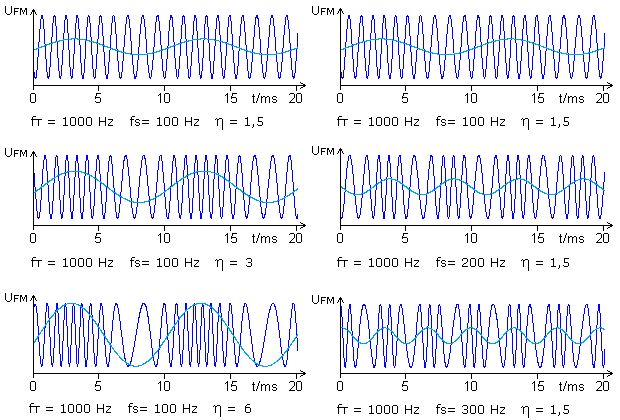
Die linken Diagramme zeigen, dass mit zunehmender NF-Amplitude, dargestellt durch die hellblaue Kurve, der Frequenzhub zunimmt. Der Hub ΔF ist die Differenz zwischen der höchsten und niedrigsten Momentanfrequenz im FM-Signal. Die höchsten Frequenzen im FM-Signal werden dem Bereich der positiven NF-Amplitude und der niedrigste Wert dem Spitzenwert der negativen Signalhalbwelle zugeordnet. Die Diagramme rechts zeigen, dass bei konstanter Signalamplitude die Häufigkeit der Frequenzwechsel zwischen maximaler und minimaler Momentanfrequenz im FM-Signal direkt von der NF-Frequenz abhängt. Bei einem stetigen Frequenzwechsel zwischen beiden Eckwerten lässt sich das FM-Signal nicht durch Sinus- oder Cosinusfunktionen beschreiben.

Die Amplitude der Signalspannung, die Lautstärke, ist direkt proportional zum Frequenzhub des FM-Signals.
Die Signalfrequenz, die Tonhöhe, bestimmt die Häufigkeit der Wechsel zwischen maximaler und minimaler Momentanfrequenz des FM-Signals.

Frequenzhub

Im FM-Signal wird ein zur Trägerfrequenz symmetrisch liegender Frequenzbereich durchlaufen. Mit den beiden Eckwerten der Frequenz wird der Frequenzhub berechnet. Er kann als Spitzenhub angegeben werden, der sich eindeutig bei einem rechteckförmigen NF-Signal messen lässt, da hierbei im FM-Signal nur die beiden Eckfrequenzen auftreten. Bei sinusförmigen Signalen kann auch der Effektivhub angegeben werden, der um den Faktor √2 kleiner ist.

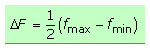
Modulationsgrad

In Analogie zur Amplitudenmodulation kann auch bei der FM ein Modulationsgrad definiert werden. Er ist als Maß der relativen Änderung des Trägersignals fT zu verstehen. Der Modulationsgrad hat keine praktische Bedeutung und darf nicht mit dem wichtigen Modulationsindex verwechselt werden.

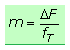
Modulationsindex

Das Verhältnis zwischen Frequenzhub und Signalfrequenz wird als Modulationsindex bezeichnet und ist eine in der Frequenzmodulation charakteristische Größe. Wie weiter oben gezeigt wurde, ist der Modulationsindex proportional zur NF-Amplitude. Zur Unterscheidung vom Modulationsgrad wird der Kennbuchstabe η, griechisch eta, vewendet.

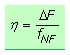
Bandbreite

Die folgenden Fourierspektren zeigen, dass die Bandbreite eines FM-Signals sehr groß sein kann. Sie ist in jedem Fall größer als der doppelte Frequenzhub. In der Praxis rechnet man mit einer endlichen Bandbreite. Darin bleiben alle außen liegenden Spektralanteile des FM-Spektrums mit Amplituden weniger als 10% der Maximalamplitude unberücksichtigt. Zur FM-Stereosignalübertragung im UKW-Rundfunkbereich muss die Bandbreite nach der Gl.2 berechnet werden. Mit ihr werden erst Spektralanteile kleiner 5% vernachlässigt, damit der Klirrfaktor im Empfangssignal unter 1% bleibt.

Im UKW-Rundfunk (Mono) beträgt der Hub 75 kHz und es werden NF-Signale mit maximal 15 kHz übertragen. Die Senderbandbreite errechnet sich nach Gl.1 zu 180 kHz und nach Gl.2 zu 210 kHz. Eine vergleichbare Amplitudenmodulation würde lediglich 30 kHz Bandbreite benötigen. Ein frequenzmoduliertes Signal hat bei Modulationsindizes über 1 eine vielfach höhere Bandbreite als eine vergleichbare Amplitudenmodulation. Eine weitere Seite befasst sich mit dem FM-Stereorundfunk auf dem UKW-Sendeband.

FM-Fourierspektren

Die Spektren sind das Ergebnis der Fourieranalyse eines Simulationsprogramms mit interner FM-Quelle bei der die Frequenzen des Trägers und des Signals sowie der Modulationsindex frei einstellbar waren.

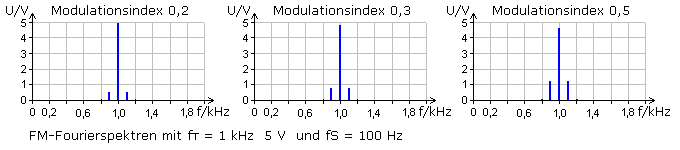
Bei kleinem Modulationsindex η ≤ 0,5 ähnelt das Spektrum dem der Amplitudenmodulation. Symmetrisch zur Trägerlinie gibt es zwei Spektrallinien im Abstand der Signal- oder Modulationsfrequenz. Dieser Frequenzabstand entspricht nicht dem Frequenzhub, der bei konstanter Signalfrequenz gleich bleibt. Die NF-Frequenzlinie ist nicht vorhanden. Anders als bei der AM ändert sich hier mit dem Modulationsindex die Amplitude des Trägers. Bei diesen kleinen Modulationsindizes kann aus dem Verhältnis der Amplitudensumme der Seitenlinien zur Trägerlinie der Wert für η errechnet werden.

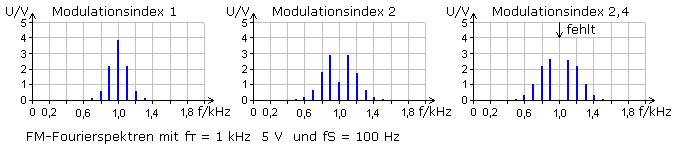
Bei größeren Modulationsindizes ab η > 0,5 treten symmetrisch zur Trägerfrequenz weitere Seitenfrequenzen auf. Sie stehen in festen Abständen von ±2·fNf, ±3·fNf  ... ±n·fNf und werden Seitenfrequenzen höherer Ordnung genannt. Ihr Abstand untereinander ist gleich der Signalfrequenz. Der Frequenzhub ist auch hier im Spektrum nicht ablesbar. Die Amplituden der Seitenlinien variieren in Abhängigkeit zum Modulationsindex. Bei η = 2,4 hat die Amplitude der Trägerlinie den Wert null, und ist im FM-Signal nicht mehr vorhanden. Aus dem Spektrum kann der Modulationsindex nicht bestimmt werden. Die Bandbreite des FM-Signals nimmt mit größerem Modulationsindex zu.

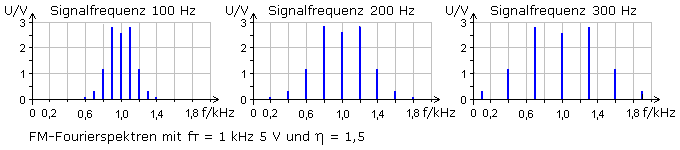
Wird bei konstantem Modulationsindex die NF-Signalfrequenz variiert, dann bestimmt sie nur den Abstand der im Spektrum auftretenden Frequenzlinien. Die Amplituden der Spektrallinien bleiben konstant.

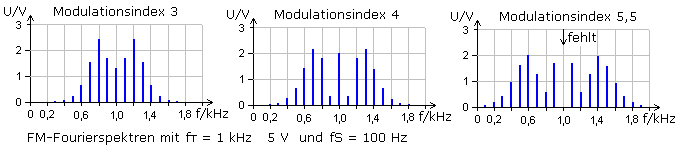
Wird bei konstanter NF-Signalfrequenz der Modulationsindex erhöht, nimmt die Zahl der Seitenlinien höherer Ordnung zu. Die Amplituden verändern sich, sind aber insgesamt kleiner. Die Trägerlinie fehlt erneut bei η = 5,5. Die in dieser Simulation gewählten Modulationsfrequenzen lassen höhere Modulationsindizes für ein unverzerrtes FM-Signal nicht mehr zu.

Die beiden Hubfrequenzen fmin = fT − ΔF sowie fmax = fT + ΔF können nur dann im Spektrum auftreten, wenn sie zufällig ein ganzzahliges Vielfaches der Informationsfrequenz sind.

Besselfunktionen und FM-Spektrum

Das recht unterschiedliche Amplitudenverhalten des Trägers und der Seitenfrequenzpaare in Abhängigkeit vom Modulationsindex ergibt sich aus dem Verlauf der Besselfunktionen. Sie zu verstehen setzt Kenntnisse der höheren Mathematik und der Lösung von Differenzialgleichungen voraus, daher werden hier nur das Ergebnis und das Zusammenwirken mit den Frequenzspektren der FM gezeigt.

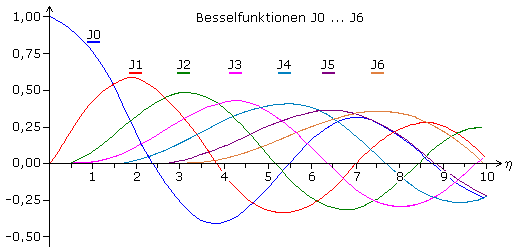
Aus dem Verlauf der J0-Kurve kann der Amplitudenwert der Trägerfrequenz in Abhängigkeit vom Modulationsindex abgelesen werden. Bei η = 2,4 ist die Trägerlinie erstmalig nicht mehr im FM-Signal enthalten. Danach erscheint sie wieder, um bei 5,5 und später bei 8,65 wieder den Wert null zu erreichen.

Durch die höheren Funktionen ab J1 werden die Amplitudenwerte der entsprechenden Seitenlinienpaare in Abhängigkeit vom Modulationsindex bestimmt. Verlaufen die Besselfunktionen im Negativen, so werden die Amplitudenwerte des Seitenlinienpaars im Fourierspektrum weiterhin positiv dargestellt. Würde man zusätzlich das Phasendiagramm darstellen, so zeigt sich dort eine Phasenverschiebung von 180°.

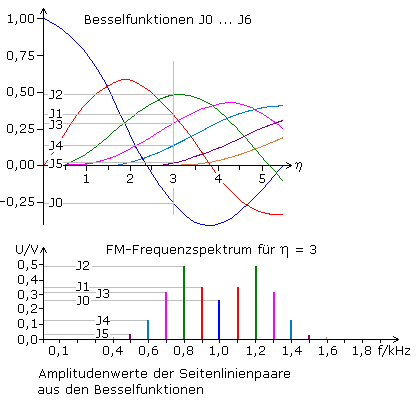
Das Diagramm zeigt den Zusammenhang zwischen den Besselfunktionen und einem FM-Spektrum. Das Spektrum wurde im Simulationsprogramm mit der Trägerfrequenz von 1 kHz und der Amplitude von 1 V erstellt. Die Modulation erfolgte mit einem Sinussignal mit f = 100 Hz bei einem Modulationsindex η = 3.

Mathematischer Hintergrund zur FM

Das Zeitdiagramm eines AM-Signals zeigt, dass die Information in den Amplitudenänderungen des Trägers liegt. Interpretiert man ebenso das Zeitdiagramm eines FM-Signals, so ist die Information in den Änderungen der Trägerfrequenz enthalten, letztlich also in den Nulldurchgängen des FM-Signals. Verändern sich die Nulldurchgänge der Trägerschwingung, so kann das auch als Phasenverschiebung oder Phasenwinkeländerung aufgefasst werden. Die Frequenzmodulation zählt wie eingangs erwähnt zur Winkelmodulation.

Wird bei der unmodulierten Trägerschwingung, also bei konstanter Kreisfrequenz, der Winkel als Funktion der Zeit φ = ω · t dargestellt, so erhält man einen linearen Anstieg. Mit ω = 2 · π · f besteht ein weiterer linearer Zusammenhang zwischen dem Phasenwinkel und der Frequenz φ = 2 · π · t · f. Das Bild zeigt für drei Frequenzen das Zeitdiagramm des Phasenwinkels.

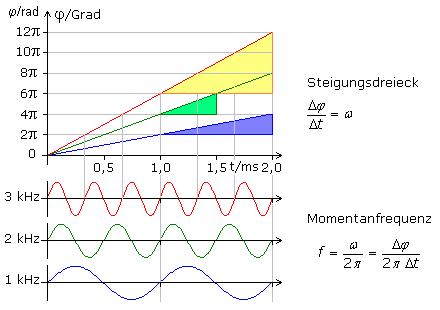
Die hervorgehobenen Steigungsdreiecke stehen für die Änderungsgeschwindigkeit der Phasenwinkel. Bei der Division durch 2·π folgt dann die Momentanfrequenz. Jedes FM-Signal hat einen nichtlinearen Phasenverlauf. Die Änderungsgeschwindigkeiten und die zugehörigen Momentanfrequenzen können wie oben ermittelt werden, wobei mathematisch genauer mit der differenziellen Größe dφ/dt zu rechnen ist.

Das folgende Bild zeigt vereinfacht die zeitliche Abhängigkeit des Phasenwinkels beim FM-Signal. Der Phasenwinkelverlauf des unmodulierten Trägers (blau) ist linear. Dieser Träger wird mit einem Cosinussignal von 0,5 kHz moduliert. Zur besseren Anschaulichkeit wurde die Signalamplitude in drei Stufen quantisiert. Der positive NF-Spitzenwert führt im FM-Signal zu 1,5 kHz und der negative Spitzenwert zu 0,5 kHz. Dazwischen bleibt der 1 kHz Träger unmoduliert. Das dabei entstehende FM-Signal ist im Zeitdiagramm zu sehen und darunter ist das modulierende Informationssignal mit den Quantisierungsstufen dargestellt.

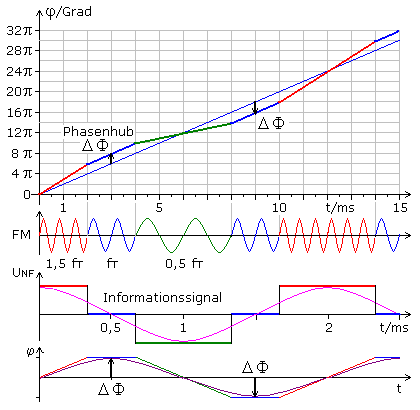
Für zwei Zeiteinheiten (0 ... 2) ms zeigt das FM-Signal 1,5 kHz, wobei drei volle Perioden entsprechend dem Bogenmaß 6π durchlaufen werden. Danach ändert sich die NF sprunghaft und für weitere zwei Zeiteinheiten (2 ... 4) ms werden 4π entsprechend der Trägerfrequenz von 1 kHz durchlaufen. Bei 4 ms ändert sich das Modulationssignal wieder sprunghaft und die FM zeigt für vier Zeiteinheiten (bis 8 ms) mit 0,5 kHz die niedrigste Momentanfrequenz. In dieser Zeit werden zwei Perioden gleich 4π durchlaufen. Danach tritt für zwei Zeiteinheiten wieder die unmodulierte Trägerfrequenz auf. Ab 10 ms springt die Frequenz für insgesamt vier Zeiteinheiten auf die höchste Momentanfrequenz, wobei sechs Perioden durchlaufen werden, ein Bogenmaß von 12π.

Das letzte Zeitdiagramm stellt die Abhängigkeit des Phasenwinkels beim FM-Signal reduziert auf den trapezförmigen Verlauf dar. Der Phasenwinkel des FM-Signals weicht um den maximalen Phasenhub ΔΦ vom Mittelwert des unmodulierten Trägers ab. Das cosinusförmige Informationssignal führt zu einem sinusförmigen Phasenhub.

Bei sinusförmiger NF-Modulationsspannung eilt das sinusförmige Phasenhubsignal um 90° nach.

Wird bei gleicher NF-Frequenz die Amplitude vergrößert, so nimmt im FM-Signal die obere Eckfrequenz zu und die untere ab, da sich der Frequenzhub vergrößert. Der Phasenhub nimmt ebenfalls zu, da bei der Maximalfrequenz pro Zeiteinheit eine höhere Anzahl und bei der Minimalfrequenz eine kleinere Anzahl von Perioden im FM-Signal durchlaufen werden.

Der maximale Frequenzhub ist proportional zum maximalen Phasenhub.  ΔF ~ ΔΦ

Wird bei konstanter Amplitude die Frequenz des modulierenden NF-Signals verändert, so wirkt sich das auf den Phasenhub aus. Die Abhängigkeit kann recht einfach mit quantisierten NF-Signalen bildlich konstruiert werden. Die beiden NF-Frequenzen unterscheiden sich um den Faktor 2. Der Phasenhub ist bei der tieferen Frequenz größer.

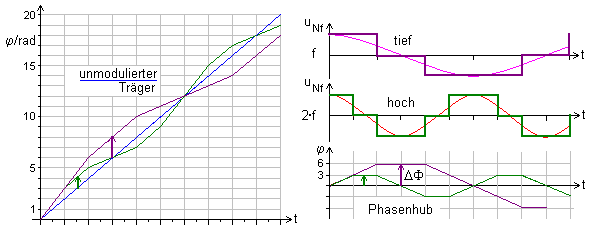
Der maximale Phasenhub ist umgekehrt proportional zur Modulationsfrequenz.    ΔΦ ~ 1 / fNf
Der maximale Phasenhub und der Modulationsindex sind gleich.    η = ΔF / fNf

Die Trägerfrequenz wird mit einem Cosinussignal moduliert und führt zu einer sinusförmigen Phasenwinkeländerung. Sie errechnet sich aus dem zeitlichen Integral über die Kreisfrequenz. Die Amplitude der Winkeländerung, der Phasenhub, ist umgekehrt proportional zur Kreisfrequenz. In mathematische Gleichungen geschrieben folgt dann die Zeitfunktion eines FM-Signals:

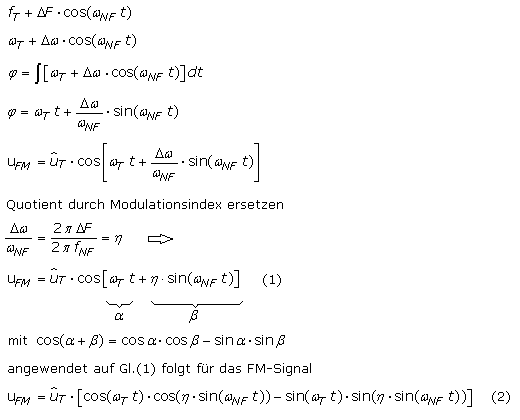
Im Klammerausdruck erscheinen Produkte verschiedener Winkelfunktion. Einen ersten Lösungsansatz findet man unter der Annahme, dass der Modulationsindex η « 1 ist. Ein Teil dieser Winkelfunktionen vereinfacht sich und auf den Rest kann wieder eine trigonometrische Beziehung angewendet werden.

Das FM-Signal setzt sich bei sehr kleinem Modulationsindex aus den drei gekennzeichneten Cosinussignalen zusammen. Das stimmt mit den zu Beginn gezeigten Fourierspektren überein, die einem AM-Spektrum ähnlich sind. In der Gleichung steht hier der Modulationsindex. Das negative Vorzeichen beim Differenzausdruck zeigt eine auf den Träger bezogene Phasenverschiebung von 90° an.

Für einen beliebigen Modulationsindex müssen die Besselfunktionen zur Berechnung eingesetzt werden. Nach der Fachliteratur "Modulationsverfahren von E. Stadler" lassen sich die Zeitfunktionen wie unten gezeigt schreiben, wobei die Amplituden Jo(η) ... Jn(η) der Spektralanteile durch die Besselfunktionen gegeben sind:

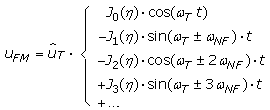
Einige Vor- und Nachteile im Vergleich zur AM

Die besonderen Vorteile der Frequenzmodulation verglichen mit der leichter zu verstehenden Amplitudenmodulation finden sich in der Störunempfindlichkeit. Fast alle Störsignale wirken auf die Amplitude, verändern aber nicht die Frequenz. Da bei der FM die Information aus der Abfolge der Signalnulldurchgänge zurück erhalten wird, bleiben Amplitudenänderungen des FM-Signals folgenlos.

Der Dynamikbereich der FM ist sehr groß und wird nur durch den Abstand zum ebenfalls modulierten Nachbarsender eingeschränkt. Der relativ große Abstand der Trägerfrequenzen der Sender auf UKW und höheren Frequenzbändern ermöglicht eine qualitativ gute NF-Übertragung, da fast deren gesamte Bandbreite genutzt werden kann. Beim FM-Rundfunk sind es 15 kHz, beim AM-Rundfunk dagegen nur 4,5 kHz. Die Einzelsignalmodulation zeigt, dass die Sendeenergiebilanz wegen vieler Seitenfrequenzpaare zugunsten des Signals ausfällt. Ein AM-Eintonsignal hat ein Seitenlinienpaar und die Amplitude des Trägers ist immer deutlich höher.

Der große Bandbreitenbedarf des FM-Signals kann ein Nachteil sein. Weiterhin lassen sich hohe NF-Frequenzen bei der Winkelmodulation (FM) schlechter übertragen, da sich der Phasenhub umgekehrt proportional zur NF verhält und dadurch die Amplituden der Seitenschwingungspaare kleiner werden. Einen Ausgleich erreicht man durch eine Preemphasis vor der Modulation. Durch sie werden die Amplituden hoher Frequenzen nichtlinear verstärkt. Ein entsprechendes Filternetzwerk im Empfänger macht diesen Vorgang nach der Demodulation weder rückgängig. Als positiven Effekt erhält man ein besseres Signal/Rauschverhältnis. Die Demodulation eines FM-Signals ist technisch aufwendiger.