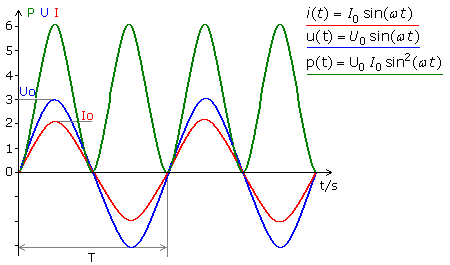
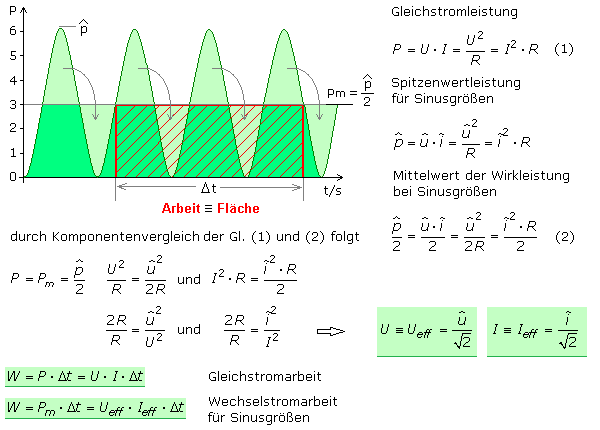
Eigenschaften von Sinussignalen
Unter diesem Titel werden neben der prinzipiellen Erzeugung eines sinusförmigen Signals auch die wichtigsten Eigenschaften der Sinussignale beschrieben. Dazu gehören der Zusammenhang zwischen Zeiger- und Liniendiagramm, der Phasenverschiebungswinkel, die Frequenz, Periodendauer und Kreisfrequenz und die Bedeutung der Effektivwerte von Sinusgrößen.
Nach den Regeln der magnetischen Induktion wird an den Anschlüssen einer Spule, die sich in einem Magnetfeld dreht, eine Spannung erzeugt. Zur Herleitung der Zusammenhänge wird hier die Spule auf eine Leiterschleife reduziert. Sie dreht sich mit konstanter Drehzahl in einem homogenen Magnetfeld, wobei in gleichen Zeitabschnitten die Änderungen des Drehwinkels gleich bleiben.
Auf eine rotierbare dünne Metallplatte treffen Magnetfeldlinien auf. Die Magnetfeldlinien mit dem magnetischen Fluss Φo durchdringen sie senkrecht. Rotiert die Metallfläche, so verändert sich die von den Feldlinien durchsetzte Größe der Fläche. Die wirksame Fläche ist die Projektion der gedrehten Fläche auf die Ebene. Dabei ändert sich auch der magnetische Fluss Φ. Sowohl die aktive Fläche als auch der damit verbundene magnetische Fluss sind Funktionen des Drehwinkels.
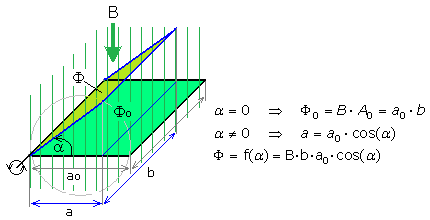
Der von der Metallplatte erfasste Magnetfluss Φ ändert sich bei gleichförmiger Drehung nach einer Cosinusfunktion.
Bei gleichförmiger Drehung kann die Winkeländerung durch die zeitliche Änderung Δt beschrieben werden. Ein voller Umlauf mit 360° entspricht einer Periode mit der Periodendauer T. Die Umlaufrichtung im Zeigerdiagramm der Elektronik ist vereinbarungsgemäß entgegen dem Uhrzeigersinn. Die Magnetflussänderung ΔΦ ist winkel- oder zeitabhängig. Die induzierte Spannung errechnet sich wie nachstehend gezeigt aus dem Induktionsgesetz. Das Ergebnis ist eine sinusförmige Spannung, bei der sich das negative Vorzeichen der Selbstinduktionsspannung aufhebt.

Aus Sicht der sich gleichmäßig drehenden Metallplatte ändert sich der Magnetfluss im Bereich 0° und 180° am stärksten, während im Bereich 90° und 270° die Flussänderungen nur noch gering sind. Das entspricht mathematisch einer Cosinusfunktion. Die Amplitude der im Metall induzierten Spannung erreicht ihren Maximalwert, wenn die größtmögliche Zahl der Feldlinien von der Platte erfasst wird. Dreht sich anstelle der Metallplatte eine Leiterschleife im Permanentmagnetfeld, dann ist die Induktionsspannung maximal, wenn in der Stellung 90° und 270° der Leiterdraht die meisten Feldlinien schneidet. Das entspricht mathematisch einer Sinusfunktion.
△Der Zusammenhang zwischen Zeiger- und Liniendiagramm
Die Darstellung sinus- oder cosinusförmiger Wechselgrößen kann sowohl im Zeiger- als auch im Liniendiagramm erfolgen. Der folgende Videoclip zeigt das für den Einheitskreis mit dem Radius der Länge 1. Wird der Kreisumfang horizontal nach rechts abgerollt, bildet er die x-Achse eines rechtwinkligen Koordinatensystems. Auf der y-Achse können dann die vom Winkel abhängigen Amplitudenwerte des Radius abgetragen werden. Bei der Rotation des Kreisradius (roter Zeiger) entgegen dem Uhrzeigersinn entsteht im Liniendiagramm eine Sinus- und Cosinuskurve. Die Zeigerlänge entspricht dem Maximal- oder Scheitelwert der Wechselgröße. Für jede Winkelstellung im Kreis ergibt sich mit dem Radius als Hypotenuse ein rechtwinkliges Dreieck.
Die Länge der grünen Kathete, die bei senkrechter Projektion des Zeigers auf die Horizontale mit φ = 0° entsteht, ist gleich dem Amplitudenwert der Cosinuskurve für den jeweiligen Winkel φ. Die Höhe des Lotes von der Zeigerspitze auf die Horizontale, die blaue senkrechte Kathetenlänge, ist gleich der Amplitude der Sinuskurve für diesen Winkel. Im Abschnitt Fachmathematik können ausführliche mathematische Herleitungen zu Winkelfunktionen des rechtwinkligen Dreiecks nachgelesen werden.
Dreht sich nach einem kompletten Umlauf der Zeiger gleichmäßig weiter, dann ist es ein periodischer Vorgang. Eine Periode umfasst 360°. Im Liniendiagramm kann die Winkeleinteilung der x-Achse durch das Bogenmaß ersetzt werden, wobei 360° dem Wert 2π entsprechen. Dieser Zusammenhang folgt aus dem Kreisumfang U mit U = 2·π·r bei r = 1.
Die Periode einer sinusförmigen Wechselgröße setzt sich aus einer positiven und negativen Halbschwingung zusammen.
△Frequenz und Periodendauer
Die Zeitdauer für einen kompletten Zeigerumlauf wird als Periodendauer bezeichnet und hat das Formelzeichen T mit der Einheit s. Die Anzahl der Perioden je Sekunde ist die Frequenz mit dem Formelzeichen f und der Einheit s−1 und wird zu Ehren des deutschen Physikers Heinrich Hertz genannt. Beide Größen sind zueinander reziprok.
Eine Frequenz von 50 Hertz besagt, dass in einer Sekunde 50 Perioden durchlaufen werden. Jede Periode besteht aus einer positiven und negativen Halbschwingung. Die Periodendauer der vollständigen Schwingung ist der 50ste Teil einer Sekunde und dauert 20 ms.
Die Kreisfrequenz
Bei bekanntem Scheitelwert U kann für jeden Winkel der Momentanwert u einer sinusförmigen Wechselgröße errechnet werden:
u = f (α) = U · sin(α)
Im Liniendiagramm kann als unabhängige Größe sowohl der Winkel α als auch die Zeit abgetragen sein. In einer Periodendauer werden 360° durchlaufen. Die Momentanwerte lassen sich daher auch in Abhängigkeit von der Zeit berechnen lassen. Im Zeigerdiagramm legt der Zeiger mit der Länge r innerhalb einer Periode den Weg s zurück:
s = 2 · π · r
Bei größerer Drehgeschwindigkeit wird der Kreisumfang und damit die Periode schneller durchlaufen. Der Zeitbegriff ist in der Umfangsgeschwindigkeit enthalten:
v = ( 2 · π · r ) / T
Die Umfangsgeschwindigkeit ist vom Radius abhängig. Dividiert man durch den Wert des Radius, wird man von r unabhängig. Der Quotient aus Umfangsgeschwindigkeit durch Radius wird
Winkelgeschwindigkeit genannt. Sie erhält als Formelzeichen ω, Omega mit der Einheit s−1:
ω = v / r = ( 2 · π ) / T
Die Winkelgeschwindigkeit ist für alle Punkte des sich drehenden Zeigers gleich groß. Die Periodendauer kann durch die Frequenz ersetzt werden. Man erhält so die in der Elektrotechnik bekanntere Beziehung der Kreisfrequenz:
ω = 2 · π · f
Die Winkelgeschwindigkeit ist die Winkeländerung pro Zeiteinheit. Der in einer bestimmten Zeit durchlaufene Winkel wird durch folgende Gleichung beschrieben:
α entspricht ω·t = 2 · π · f · t somit ist
t = α° / (f · 360°)
Sind der Scheitelwert und die Frequenz bekannt, dann ist der Momentanwert einer sinusförmigen Wechselgröße für jeden Zeitpunkt errechenbar:
u = f (t) = U · sin ( ω · t ) = U · sin ( 2 · π · f · t )
Der Phasenverschiebungswinkel
Sind in einem System mehrere sinusförmige Wechselgrößen vorhanden, so fehlt zur eindeutigen Beschreibung neben Frequenz und Scheitelwert noch der Phasenwinkel. Zwei Sinusschwingungen gleicher Frequenz sollen zeitlich zueinander verschoben sein. Das Bild zeigt eine Momentaufnahme im Zeiger- und Liniendiagramm, wobei keine Schwingung zum Zeitpunkt t = 0 entsprechend φ = 0 mit dem Winkel φ = 0° beginnt.
In Liniendiagramm hat die blaue Kurve bei φ = 0° einen positiven und die rote Kurve einen negativen Amplitudenwert. Werden diese Werte auf das Zeigerdiagramm projiziert, so lassen sich die entsprechenden Zeiger einzeichnen und die Winkelwerte bei diesen Amplituden ablesen. Als Bezugswinkel oder Bezugsphase werden 0° festgelegt. Der Phasenwinkel der blauen Kurve beträgt φ1 = +30°. Der Phasenwinkel der roten Kurve beträgt φ2 = −45°. Diese Winkel werden als Nullphasenwinkel bezeichnet und sind vom Bezugspunkt abhängig. Der Phasenverschiebungswinkel ist die Differenz der Nullphasenwinkel und unabhängig vom gemeinsamen Bezugspunkt. Er errechnet sich zu absolut φ = 75°.
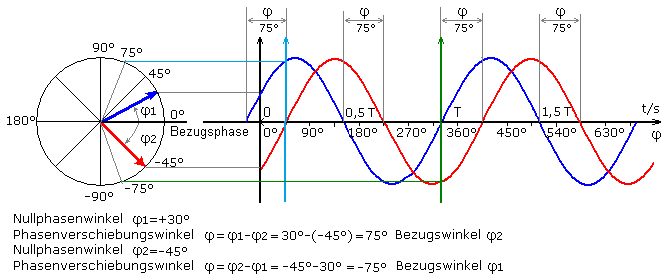
Wird die Amplitudenachse nach rechts auf die grüne Position verschoben, dann beginnt die blaue Kurve im Nullpunkt und wird zur Bezugskurve. Die rote Kurve hat zu diesem Zeitpunkt eine negative Amplitude. Der zugehörige Winkel kann im Zeigerdiagramm mit φ = −75° abgelesen werden. Von dieser Stelle aus betrachtet erreicht im Liniendiagramm die rote Kurve den Amplitudenwert 0 nach Ablauf von 75°. Die rote Kurve eilt der blauen Bezugskurve um diesen Phasenverschiebungswinkel nach, daher das Minuszeichen für den Phasenwinkel mit φ = −75°.
Soll dagegen die rote Kurve als Bezugskurve dienen, so wird die Amplitudenachse zur hellblauen Position verschoben. Die blaue Kurve hat dort schon eine positive Amplitude, für die im Zeigerdiagramm der Phasenwinkel φ = 75° abgelesen werden kann. Im Liniendiagramm hatte die blaue Kurve vor 75° den Amplitudenwert 0 bei positiver Steigung. Die blaue Kurve eilt der Bezugskurve vor, daher das Pluszeichen für den Phasenwinkel mit φ = +75°.
△