Verhalten belasteter passiver RC-Pässe
Eine passive RC-Schaltung kann als Hoch- oder Tiefpass-Filter genutzt werden. Beim RC-Hochpass liegt das Ausgangssignal parallel zum Widerstand und beim RC-Tiefpass parallel zum Kondensator. Die Kombination passend dimensionierter Hoch- und Tiefpass-Filter ergeben einen Bandpass oder eine Bandsperre. Die Berechnung der Grenzfrequenz und die Übertragungsfunktion gilt nur für einfache unbelastete Pass- oder Filterschaltung. In kombinierten Filterschaltungen belasten sich die Aus- und Eingänge der einfachen HP- oder TP-Glieder gegenseitig. Das hat Einfluss auf die Ergebnisse der jeweiligen Übertragungsfunktion. Im Folgenden werden die RC-Pässe nur mit Wirkwiderständen belastet. Die mathematischen Herleitungen gelten angepasst auch für RL-Pässe und kombinierte Schaltungen.
Grenzfrequenzversatz belasteter Tiefpässe
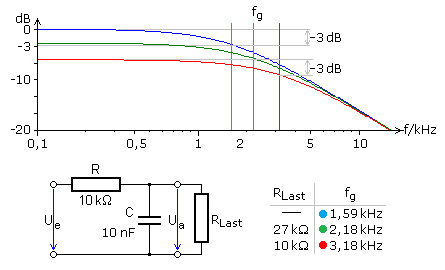
Ist ein RC-Tiefpass am Ausgang durch den Wirkwiderstand einer Folgeschaltung belastet, so wird mit zunehmender Belastung die Nutzspannung kleiner und die Grenzfrequenz nimmt höhere Werte an.
Unverändert bleibt die Dämpfung der Ausgangsamplitude bei Grenzfrequenz von −3 dB für einen passiven Pass 1. Ordnung. Das Diagramm zeigt die Simulationsergebnisse für einen
RC-Tiefpass.
Zur Berechnung der Grenzfrequenz eines belasteten Passes wird die bekannte Formel erweitert. Für die Signalquelle soll ideales Verhalten mit einem 0Ω Innenwiderstand angenommen werden.
Auf das Signal bezogen bilden der Lastwiderstand und der Tiefpasswiderstand eine Parallelschaltung. Für sie wird ein Ersatzwiderstand berechnet mit dem die neue Grenzfrequenz berechnet wird:
\[{R_{ers}} = \frac{{R \cdot {R_{Last}}}}{{R + {R_{Last}}}}\quad \quad {f_g} = \frac{1}{{2\,\pi \,{R_{ers}}\,C}}\]
Die mit dieser Formel berechneten Grenzfrequenzen werden von den Messergebnissen einer Simulationsschaltung bestätigt.
| RLast/kΩ |
Rers/kΩ |
Ua/mV |
fg/kHz |
Ua/Ue/dB |
| - |
- |
707 |
1,591 |
-3,0 |
| 27 |
7,297 |
516 |
2,181 |
-5,7 |
| 10 |
5,0 |
353 |
3,183 |
-9,0 |
Ist der Innenwiderstand der Signalquelle nicht zu vernachlässigen, so wird sein Wert zum Tiefpasswiderstand R addiert. Auf das Signal bezogen bilden diese beiden Widerstände eine Reihenschaltung.
Je größer der Wert des Innenwiderstand ist, desto niedriger wird die Grenzfrequenz.
Grenzfrequenzversatz belasteter Hochpässe
Auch beim passiven RC-Hochpass haben der Innenwiderstand der Signalquelle und eine Ausgangslast Einfluss auf die Grenzfrequenz und das Übertragungsverhalten. Wird der Innenwiderstand in die Rückleitung zur Quelle gezeichnet, dann bildet die Ausgangsparallelschaltung R || RLast mit dem Innenwiderstand Ri der Quelle eine Reihenschaltung.
Der Ersatzwiderstand zur Berechnung der neuen Grenzfrequenz ist dann die Addition der Widerstandswerte. Der Innenwiderstand der Signalquelle kann vernachlässigt werden, wenn er verglichen mit dem Wert des Ausgangswiderstands des Hochpasses klein genug ist.
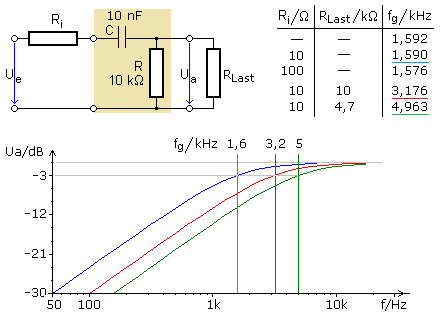
Die Simulationsergebnisse zeigen, dass mit zunehmender Belastung die Grenzfrequenz in den höheren Bereich verschoben wird. Die Grenzfrequenz für den belasteten RC-Hochpasses kann mit dem folgenden Ersatzwiderstand berechnet:
\[{R_{ers}} = {R_i} + \frac{{R\,{R_{Last}}}}{{R + {R_{Last}}}}\quad \quad {f_g} = \frac{1}{{2\,\pi \,{R_{ers}}\,C}}\]
Übertragungsfunktion für einen belasteten RC-Tiefpass
Mithilfe der komplexen Wechselstromrechnung können viele Berechnungen einfacher ohne umfangreiche Zeigerdiagramme durchgeführt werden. Mit einer Übertragungsfunktion kann der Amplituden- und Phasenfrequenzgang berechnet werden. Die prinzipielle Vorgehensweise wird am RC-Tiefpass gezeigt. Die Signalquelle wird als ideal angenommen. Der RC-Tiefpass wird durch einen Wirkwiderstand belastet und stellt eine gemischte Reihen-Parallel-Schaltung dar.
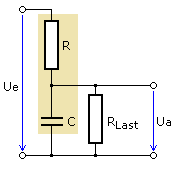
Die Ausgangsspannung liegt an der Parallelschaltung des Kondensators mit dem Lastwiderstand. Für die Impedanz der Parallelschaltung gilt:
\[\underline Z = \frac{{{R_{Last}} \cdot \frac{1}{{j\,\omega \,C}}}}{{{R_{Last}} + \frac{1}{{j\,\omega \,C}}}} = \frac{{{R_{Last}}}}{{1 + j\,\omega \,{R_{Last}}\,C}}\quad (1)\]
Die Übertragungsfunktion ist das Verhältnis der Ausgangsspannung an Z zur Eingangsspannung die an der Reihenschaltung des Wirkwiderstands R und der komplexen Impedanz Z liegt.
Da bei einer passiven Schaltung die Ausgangsspannung nie größer als die Eingangsspannung sein kann, wird die Übertragungsfunktion meistens auf die Ausgangsspannung normiert indem durch den Zählerausdruck dividiert wird. Angewendet auf die Gl.(1) ergibt sich:
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{{\underline Z }}{{R + \underline Z }} = \frac{1}{{1 + \frac{R}{{\underline Z }}}}\;\;\, \Rightarrow \;\;\,\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{1}{{1 + \frac{{R\,(1 + j\,{\mkern 1mu} \omega \,{\mkern 1mu} C\,{\mkern 1mu} {R_{Last}})}}{{{R_{Last}}}}}}\]
Der Nennerausdruck wird auf einen Hauptnenner gebracht und die Gleichung konjugiert komplex erweitert:
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{{\frac{{R + {R_{Last}}}}{{{R_{Last}}}} - j\,\omega \,R\,C}}{{{{\left( {\frac{{R + {R_{Last}}}}{{{R_{Last}}}}} \right)}^2} + {{(\omega \,R\,C)}^2}}}\]
Die Übertragungsfunktion aufgeteilt in ihre Komponentenform geschrieben ergibt die Gleichung Gl.(2):
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{{\frac{{R + {R_{Last}}}}{{{R_{Last}}}}}}{{{{\left( {\frac{{R + {R_{Last}}}}{{{R_{Last}}}}} \right)}^2} + {{(\omega \,R\,C)}^2}}} - j\left[ {\frac{{\omega \,R\,C}}{{{{\left( {\frac{{R + {R_{Last}}}}{{{R_{Last}}}}} \right)}^2} + {{(\omega \,R\,C)}^2}}}} \right]\]
Mit der Gl.(2) wird der Betrag des Amplitudenfrequenzgangs berechnet zu:
werden. Dazu sind die Real- und Imaginärkomponente zu quadrieren und aus der Summe wird die Quadratwurzel gezogen:
\[\left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| = \sqrt {{{{\mathop{\rm Re}\nolimits} }^2} + {{{\mathop{\rm Im}\nolimits} }^2}} \]
\[\left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| = \frac{1}{{\sqrt {{{\left( {\frac{{R + {R_{Last}}}}{{{R_{Last}}}}} \right)}^2} + {{(\omega \,R\,C)}^2}} }}\quad (3)\]
Die einzige Variable in der Gl.(3) ist die Frequenz. Die Grenzwertbetrachtungen mit f → 0 und f →∞ zeigen das Tiefpassverhalten:
\[\omega \to 0\quad \left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| \to \frac{{{R_{Last}}}}{{R + {R_{Last}}}}\quad \quad \omega \to \infty \quad \left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| \to 0\]
Die Abhängigkeit des Phasenwinkels von der Frequenz errechnet sich aus dem Arcustangens des Quotienten aus der Imaginär- zur Realkomponente. Die Phasenlage der Eingangsspannung hat per Definition null Grad. Das negative Vorzeichen in der Gl.(4) zeigt, dass es sich um einen Tiefpass handelt.
\[\varphi (\omega ) = {\mathop{\rm arc}\nolimits} \,tan\left( {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right)\quad \quad \varphi (\omega ) = {\mathop{\rm arc}\nolimits} \,tan\left( {\frac{{ - \omega \,R\,C}}{{\frac{{R + {R_{Last}}}}{{{R_{Last}}}}}}} \right)\]
\[\varphi (\omega ) = - {\mathop{\rm arc}\nolimits} \,tan\left( {\frac{{\omega \,{R_{Last}}\,R\,C}}{{R + {R_{Last}}}}} \right)\quad (4)\]
Bei der Grenzfrequenz beträgt der Absolutwert des Phasenwinkels immer |φ| = 45°. Aus dem Argument der Gl.(4) kann somit die Grenzfrequenzformel für den belasteten Tiefpass hergeleitet werden. Sie ist identisch mit der eingangs benutzten Formel für den Ersatzwiderstand Rers.
\[\varphi = - {45^o} = - {\mathop{\rm arc}\nolimits} \,tan(1)\quad \Rightarrow \quad \frac{{{R_{Last}}\,R}}{{R + {R_{Last}}}}\omega \,C = 1\]
\[{R_{ers}} = \frac{{{R_{Last}}\,R}}{{R + {R_{Last}}}}\quad \Rightarrow \quad {f_g} = \frac{1}{{2\,\pi \,{R_{ers}}\,C}}\]
Übertragungsfunktion für einen belasteten RC-Hochpass
Zur einfacheren Herleitung soll der Hochpass nur durch einen Wirkwiderstand belastet werden. Die Ausgangsspannung liegt an der Parallelschaltung aus HP-Widerstand und Lastwiderstand. In der Übertragungsfunktion ist er als Parallelwiderstand Rp bezeichnet. Der Innenwiderstand der Quelle Ri bildet mit ihm eine Reihenschaltung.
Bei gemischter Ausgangsbelastung mit Impedanzen ist die komplexe Wechselstromrechnung die einzig brauchbare Methode.
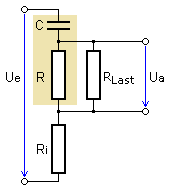
Für den dargestellten Hochpass gilt die allgemeine und anschließend normierte Übertragungsfunktion:
\[{R_p} = \frac{{R\,{R_{Last}}}}{{R + {R_{Last}}}}\quad \quad \frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{{{R_p}}}{{({R_i} + {R_p}) - \frac{j}{{\omega \,C}}}}\]
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{1}{{\frac{{{R_i} + {R_p}}}{{{R_p}}} - j\frac{1}{{\omega \,{R_p}\,C}}}}\]
Mithilfe der konjugiert komplexen Erweiterung wird der Nennerausdruck real. Die Übertragungsfunktion kann in die Real- und Imaginärkomponente getrennt geschrieben werden:
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{{\frac{{{R_i} + {R_p}}}{{{R_p}}}}}{{{{\left( {\frac{{{R_i} + {R_p}}}{{{R_p}}}} \right)}^2} + {{\left( {\frac{1}{{\omega \,{R_p}\,C}}} \right)}^2}}} + \left[ {\frac{{\frac{1}{{\omega \,{R_p}C}}}}{{{{\left( {\frac{{{R_i} + {R_p}}}{{{R_p}}}} \right)}^2} + {{\left( {\frac{1}{{\omega \,{R_p}\,C}}} \right)}^2}}}} \right] \cdot j\]
Damit kann der Phasengang bestimmt werden:
\[\varphi (\omega ) = {\mathop{\rm arc}\nolimits} \,tan\left[ {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right] = \frac{{\frac{1}{{\omega \,{R_p}C}}}}{{\frac{{{R_i} + {R_p}}}{{{R_p}}}}} = \frac{1}{{({R_i} + {R_p})\,\omega \,C}}\]
\[\varphi (\omega ) = {\mathop{\rm arc}\nolimits} \,tan\left[ {\frac{1}{{\left( {{R_i} + \frac{{R\,{R_{Last}}}}{{R + {R_{Last}}}}} \right)\omega \,C}}} \right]\]
Das positive Vorzeichen zeigt, dass es sich um einen Hochpass handelt. Für φ = 45° hat der Hochpass seine Grenzfrequenz mit der Formel:
\[{f_g} = \frac{1}{{2\,\pi \,\left( {{R_i} + \frac{{R\,{R_{Last}}}}{{R + {R_{Last}}}}} \right)\,C}}\]
Die weiter oben ermittelten Simulationsergebnisse können mit diesen Formeln bestätigt werden.
△
RC-Bandpässe
Hoch- und Tiefpässe haben eine charakteristische Grenzfrequenz. Sie trennt idealisiert den Durchlass- vom Sperrbereich. Es sollte möglich sein durch Zusammenschalten beider Pässe aus einem breiten Frequenzband einen schmaleren Frequenzbereich herauszufiltern. Vielleicht gibt es zwei Ergebnisse, wo im Ausgangssignal nur das schmale Frequenzband enthalten ist oder wo es fehlt. Der erste Fall wird Bandpass, der letzte Fall Bandsperre genannt. Das Kapitel passive elektrische Filter enthält dazu allgemein gehaltene Informationen. Nachfolgend werden hier einfache passive RC-Pässe in Reihe geschaltet.
1. Schaltungsvariante
Ein RC-Tiefpass bildet mit einem RC-Hochpass eine Reihenschaltung. Die Ausgangsspannung liegt am Kondensator vom TP und ist das Eingangssignal für den folgenden HP. Das Ausgangssignal des gesamten Filters liegt am Widerstand vom HP. Beide Pässe sind gleich dimensioniert und haben die gleiche Grenzfrequenz. Für niedrige Eingangsfrequenzen unterhalb der Grenzfrequenz sind die Kondensatoren hochohmig. Am TP-Ausgang ist die Spannung hoch, wird aber vom nachfolgenden Hochpass stark gedämpft. Die Ausgangsamplitude des Filters am HP-Widerstand ist klein. Für hohe Eingangsfrequenzen oberhalb der Grenzfrequenz sind die Kondensatoren niederohmig. Am TP-Ausgang ist die Spannungsamplitude stark gedämpft und wird vom nachfolgenden HP fast nicht gedämpft. Die Ausgangsamplitude des Filters am HP-Widerstand ist hoch. Bei der Grenzfrequenz, die für beide Filter identisch sein soll, sind die Wirk- und Blindwiderstände beider Pässe gleich groß. Für die Ausgangsspannung ist die höchste Spannungsamplitude zu erwarten.
2. Schaltungsvariante
In der Reihenschaltung ändert sich die Position der beiden Pässe. Das Eingangssignal liegt am HP und das Ausgangssignal wird am nachfolgenden TP abgenommen. Eingangsfrequenzen unterhalb der Grenzfrequenz werden vom hochohmigen HP-Kondensator gedämpft und können am TP-Kondensator des Filterausgangs nur diese niedrigen Spannungswerte ergeben. Eingangsfrequenzen oberhalb der Grenzfrequenz gelangen mit hoher Spannungsamplitude an den nachfolgenden TP, dessen Ausgangskondensator aber mit seinem niederohmigen TP-Kondensator die Ausgangsspannung des Filters zunehmend dämpft. Im Bereich der Grenzfrequenz ist die Ausgangsspannung des Filters am größten.
Simulationsmessungen
Für beide Schaltungsvarianten wurden im Simulationsprogramm die Bodediagramme aufgenommen. Sie sind identisch. Die Bauteilwerte und die Messwerte der charakteristischen Frequenzen sind angegeben.
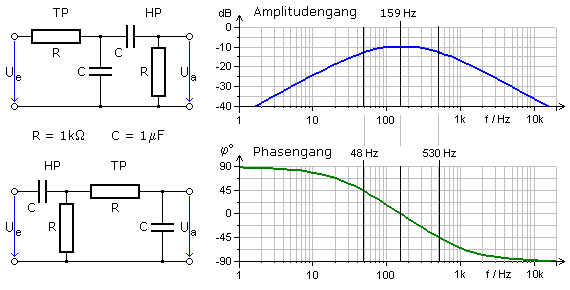
Im Beispiel hat der Bandpass bei fgu = 48 Hz seine untere Grenzfrequenz. Der abgelesene Phasenwinkel beträgt dort φ = +45°. Ein positiver Phasenwinkel steht in Verbindung zum Hochpass. Die obere Grenzfrequenz des Filters beträgt fgo = 530 Hz bei φ = −45° und wird somit vom Tiefpass bestimmt. Im Durchlassbereich gemessen hat die Maximalamplitude −9,5 dB. Das ist nur noch ein Drittel der Durchlassamplitude des einzelnen Hoch- oder Tiefpasses. Beide Pässe beeinflussen sich gegenseitig, da die Ausgangsimpedanz des einen die Eingangsimpedanz des anderen belastet und umgekehrt.
Die Serienschaltung von Hoch- und Tiefpass ergibt nur dann einen sinnvoll nutzbaren Bandpass, wenn die Grenzfrequenz des HP gleich oder niedriger als die des TP ist. Ein identisches Ergebnis wird erreicht, wenn die Grenzfrequenz des TP gleich oder höher der des HP ist. Ist unter diesen Voraussetzungen das Verhältnis der beiden Grenzfrequenzen 1:10, dann ist die Dämpfung bei der Mittenfrequenz mit -1,6 dB geringer als bei gleichen Grenzfrequenzen. Die Bandbreite ist deutlich größer als beim Grenzfrequenzverhältnis 1:1.
Die Bandbreite ist definiert als Differenz zwischen der oberen und unteren Grenzfrequenz. Sind die Werte bekannt, so kann daraus die Mittenfrequenz fo des Filters wie folgt berechnet werden:
\[B = \Delta f = {f_{go}} - {f_{gu}}\quad \quad {f_o} = \sqrt {{f_{go}} \cdot {f_{gu}}} \]
Die gegenseitige Belastung von Hoch- und Tiefpass kann durch einen Impedanzwandler verhindert werden. Mit seiner sehr hohen Eingangsimpedanz belastet er den Ausgang des vorgeschalteten HP nicht.
In der Grundschaltung hat der Impedanzwandler den Verstärkungsfaktor 1 und keinen Einfluss auf die Signalamplitude. Seine Ausgangsimpedanz ist sehr niedrig und stellt für den folgenden TP eine fast ideale Signalquelle dar. Die Diagramme der Simulationsschaltung zeigen den Bandpasscharakter mit gleicher Mittenfrequenz. Infolge der Entkopplung ist die Durchlassamplitude mit −6 dB weniger stark gedämpft. Die Bandbreite ist geringer und das Filterverhalten optimaler.
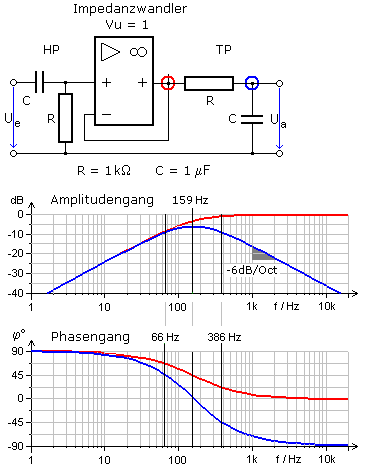
Der rote Kurvenzug am Ausgang des Impedanzwandlers zeigt das Bodediagramm des nicht belasteten HP mit der Grenzfrequenz von 159 Hz. Auf die Amplitude der Eingangsspannung bezogen lassen sich
−3 dB ablesen. Der folgende Tiefpass mit gleicher Grenzfrequenz dämpft diese Amplitude um den gleichen Wert. Die Maximalamplitude des Bandpasses erreicht somit −6 dB.
Mit weiter zunehmender Frequenz dämpft der TP seine Ausgangsamplitude mit 6 dB pro Oktave oder 20 dB pro Dekade. Es handelt sich damit um ein Filter 1. Ordnung.
Die Entkopplung mit einem Impedanzwandler wird oft angewendet, zumal er auch unter Beibehalten seiner günstigen Ein- und Ausgangsimpedanzen zum Verstärker erweitert werden kann.
Die gesamte Filterschaltung ist nicht mehr passiv, da der Operationsverstärker eine symmetrische DC-Betriebsspannung benötigt.
Komplexe Übertragungsfunktion für den RC-Bandpass
Die Berechnungen für einen passiven Bandpass sollten mit komplexer Wechselstromrechnung erfolgen, da Signale mit unterschiedlichen Phasenwinkeln auf Impedanzen treffen, die ihrerseits von der Frequenz abhängige Spannungsteiler bilden. Der Bandpass ist als Spannungsteiler dargestellt und die einzelnen Pässe sind farblich gekennzeichnet. Der Innenwiderstand der AC-Quelle wird als vernachlässigbar klein angenommen.
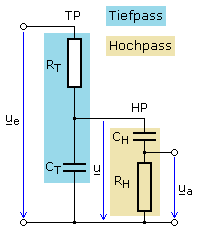
Für die HP-Impedanz gilt:
\[{\underline Z _{hp}} = {R_H} + \frac{1}{{j\,\omega \,{C_H}}}\]
Der Blindwiderstand des TP wird durch Zhp belastet. Für die Impedanz der Parallelschaltung gilt:
\[{\underline Z _{par}} = \frac{{\frac{1}{{j\,\omega \,{C_T}}} \cdot {{\underline Z }_{hp}}}}{{\frac{1}{{j\,\omega \,{C_T}}} + {{\underline Z }_{hp}}}} = \frac{{{{\underline Z }_{hp}}}}{{1 + {{\underline Z }_{hp}} \cdot j\,\omega \,{C_T}}}\]
Der Bandpass BP ist der am Ausgang durch den HP belastete TP. Für die Gesamtimpedanz des BP gilt:
\[{\underline Z _{bp}} = {R_T} + {\underline Z _{par}} = {R_T} + \frac{{{{\underline Z }_{hp}}}}{{1 + {{\underline Z }_{hp}} \cdot j\,\omega \,{C_T}}}\]
Für den Bandpass kann die Herleitung der Übertragungsfunktion auf zwei Wegen erfolgen. Für den belasteten TP und den nachfolgenden HP werden die getrennten Übertragungsfunktionen aufgestellt und miteinander multipliziert. Dabei kürzt sich die mittlere Spannung u heraus. Das Ergebnis ist die Übertragungsfunktion für den Bandpass. Für den Bandpass wird die Gesamtimpedanz hergeleitet und das normierte Spannungsverhältnis von ua am HP-Widerstand zu ue am BP-Eingang berechnet. Beide Varianten erfordern bei der Herleitung viele Zwischenschritte.
Die Herleitung erfolgt mit getrennten Übertragungsfunktionen und unterschiedlichen Bauteilwerten für den HP und TP. Für die normierte Übertragungsfunktion des HP gilt:
\[{\underline Z _{hp}} = {R_H} + \frac{1}{{j\,\omega \,{C_H}}}\]
Für die Übertragungsfunktion des belasteten TP gilt:
\[\frac{{\underline u }}{{{{\underline u }_e}}} = \frac{{{{\underline Z }_{par}}}}{{{{\underline Z }_{bp}}}} = \frac{{{{\underline Z }_{par}}}}{{{R_T} + {{\underline Z }_{par}}}}\]
Mit einigen Zwischenschritten wird Zpar durch Einsetzen der HP-Impedanz Zhp umgeformt:
\[{\underline Z _{par}} = \frac{{{R_H} + \frac{1}{{j\,\omega \,{C_H}}}}}{{1 + \left( {{R_H} + \frac{1}{{j\,\omega \,{C_H}}}} \right) \cdot j\,\omega \,{C_T}}} = \frac{{{R_H} + \frac{1}{{j\,\omega \,{C_H}}}}}{{1 + j\,\omega \,{R_H}\,{C_H} + \frac{{j\,\omega \,{C_T}}}{{j\,\omega \,{C_H}}}}}\]
Kürzen im Nenner und danach den Zähler und Nenner durch RH dividieren ergibt:
\[{\underline Z _{par}} = \frac{{1 + \frac{1}{{j\,\omega \,{R_H}\,{C_H}}}}}{{\frac{1}{{{R_H}}} + j\,\omega \,{C_H} + \frac{{{C_T}}}{{{R_H}\,{C_H}}}}}\]
Mit dieser Formel kann die Impedanz für den Bandpass aufgestellt werden:
\[{\underline Z _{bp}} = {R_T} + {\underline Z _{par}} = {R_T} + \frac{{1 + \frac{1}{{j\,\omega \,{R_H}\,{C_H}}}}}{{\frac{1}{{{R_H}}} + \frac{{{C_T}}}{{{R_H}\,{C_H}}} + j\,\omega \,{C_H}}}\]
Die Formel wird mit dem Hauptnenner geschrieben zu:
\[{\underline Z _{bp}} = \frac{{{R_T}\left( {\frac{1}{{{R_H}}} + \frac{{{C_T}}}{{{R_H}\,{C_H}}} + j\,\omega \,{C_H}} \right) + 1 + \frac{1}{{j\,\omega \,{R_H}\,{C_H}}}}}{{\frac{1}{{{R_H}}} + \frac{{{C_T}}}{{{R_H}\,{C_H}}} + j\,\omega \,{C_H}}}\]
Im Zähler wird der Klammerausdruck aufgelöst und mit \(1/j\,\omega \,{R_H}\,{C_H} = - j/\omega \,{R_H}\,{C_H}\) weiter umgeformt zu:
\[{\underline Z _{bp}} = \frac{{1 + \frac{{{R_T}}}{{{R_H}}} + \frac{{{R_T}\,{C_T}}}{{{R_H}\,{C_H}}} + j\left( {\omega \,{R_T}\,{C_H} - \frac{1}{{\omega \,{R_H}\,{C_H}}}} \right)}}{{\frac{1}{{{R_H}}} + \frac{{{C_T}}}{{{R_H}\,{C_H}}} + j\,\omega \,{C_H}}}\]
Wird jetzt die Übertragungsfunktion für den belasteten TP aufgestellt, kann gekürzt werden und es bleibt:
\[\frac{{\underline u }}{{{{\underline u }_e}}} = \frac{{{{\underline Z }_{par}}}}{{{{\underline Z }_{bp}}}} = \frac{{1 + \frac{1}{{j\,\omega \,{R_H}\,{C_H}}}}}{{1 + \frac{{{R_T}}}{{{R_H}}} + \frac{{{R_T}\,{C_T}}}{{{R_H}\,{C_H}}} + j\left( {\omega \,{R_T}\,{C_H} - \frac{1}{{\omega \,{R_H}\,{C_H}}}} \right)}}\]
Es muss mit der HP-Übertragungsfunktion multipliziert werden. Für die normierte Formel gilt:
\[\frac{{{{\underline u }_a}}}{{\underline u }} = \frac{{{R_H}}}{{{{\underline Z }_{hp}}}} = \frac{1}{{1 + \frac{1}{{\omega \,{R_H}\,{C_H}}}}}\]
Bei der Multiplikation der einzelnen Übertragungsfunktionen kann gekürzt werden. Das Ergebnis ist die gesuchte Übertragungsfunktion für den allgemeinen Bandpass:
\[\frac{{\underline u }}{{{{\underline u }_e}}} \cdot \frac{{{{\underline u }_a}}}{{\underline u }} = \frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{1}{{1 + \frac{{{R_T}}}{{{R_H}}} + \frac{{{R_T}\,{C_T}}}{{{R_H}\,{C_H}}} + j\left( {\omega \,{R_T}\,{C_H} - \frac{1}{{\omega \,{R_H}\,{C_H}}}} \right)}}\]
Oftmals sind komplexe Herleitungen für den Amplituden- und Phasenfrequenzgang für Bandpässe mit gleichartig dimensionierten Bauteilen zu finden.
Mit RH = RT = R und CH = CT = C wird die BP-Übertragungsfunktion anschaulicher:
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{1}{{3 + j\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right)}}\]
In Komponentenform geschrieben können die entsprechenden Formeln für den Amplituden- und Phasengang aufgestellt werden:
\[\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}} = \frac{3}{{9 + {{\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right)}^2}}} - \left[ {\frac{{\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}}}{{9 + {{\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right)}^2}}}} \right] \cdot j\]
Amplituden- und Phasengang
Der Amplitudengang ist das Ergebnis der Wurzel aus der Summe der Quadrate der Real- und Imaginärkomponente (ohne j):
\[\left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| = \frac{1}{{\sqrt {9 + {{\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right)}^2}} }}\]
Bei der Mittenfrequenz der gleichwertig dimensionierten Bandpassschaltung mit \({\omega _o} = 1/(R\,C)\) hat die Imaginärkomponente den Wert null. Das per Schaltungssimulation erhaltene Bodediagramm zeigt bei der Mittenfrequenz den Phasenwinkel \(\varphi = {0^o}\) und bestätigt die Aussage. Für die Mittenfrequenz fo des passiven symmetrisch dimensionierten Bandpass und seine maximale Amplitude bei fo gilt:
\[{f_o} = \frac{1}{{2\,\pi \,R\,C}}\quad \quad \left| {\frac{{{{\underline u }_a}}}{{{{\underline u }_e}}}} \right| = \frac{1}{3} \equiv - 9,54\,dB\]
Der Phasengang errechnet sich aus dem Arcustangens des Verhältnisses der Imaginär- zur Realkomponente der Übertragungsfunktion:
\[\varphi (\omega ) = - {\mathop{\rm arc}\nolimits} \,tan\left[ {\frac{1}{3}\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right)} \right]\]
Bei den Grenzfrequenzen hat der Phasenwinkel den absoluten Wert φ = 45° und somit ist \(\left| {{\mathop{\rm arc}\nolimits} \,tan({{45}^o})} \right| = 1\). Für die Grenzwerte kann eine quadratische Gleichung aufgestellt werden, die mithilfe der quadratischen Ergänzung Lösungsformeln für die beiden absoluten Frequenzwerte liefert:
\[\frac{1}{3}\left( {\omega \,\,R\,\,C - \frac{1}{{\omega \,\,R\,\,C}}} \right) = 1\quad \Rightarrow \quad {(\omega \,\,R\,\,C)^2} - 3\,(\omega \,\,R\,\,C) = 1\]
\[{f_{1,2}} = \frac{1}{{2\,\pi \,R\,C}} \cdot \left| {\left( {\frac{3}{2} \pm \sqrt {1 + \frac{9}{4}} } \right)} \right|\]
\[{f_1} = \frac{{3,3028}}{{2\,\pi \,R\,C}} = {f_{go}}\quad \quad {f_2} = \frac{{0,3028}}{{2\,\pi \,R\,C}} = {f_{gu}}\]
Mit den zur Simulation gewählten Bauteilwerten errechnet sich die Mittenfrequenz zu f0 = 159 Hz. Mit f1 = 525 Hz als obere und f2 = 48 Hz als untere Grenzfrequenz stimmen die abgelesenen Diagrammwerte sehr gut überein. Ein spezieller RC-Bandpass ist das in einem eigenen Kapitel ausführlich beschriebene Wienglied. Eine Schaltung, die in analogen Sinusgeneratoren oft Verwendung fand und sich durch eine sehr gute Signalqualität auszeichnet.






