Passive elektrische Filterschaltungen
Unter diesem Titel werden passive Bandpass- und Bandsperrfilter gezeigt, deren Schaltungen RC- und RL-Glieder aufweisen. Ein in der Unterhaltungselektronik genutztes Filter ist das Klangeinstellnetzwerk, dass sowohl in passiver als auch in aktiver Schaltungsvariante eingesetzt wird. Bessere Filtereigenschaften werden mit T- und Pi-Filterschaltung erreicht, die in ihren Grundschaltungen gezeigt werden. Eine große Filtergruppe ist aus LC-Grundhalbgliedern aufgebaut, die dann als eingliedrige LC-Grundketten in vielen LC-Bandfiltern für Selektivverstärker zu finden sind. Als spezielle LC-Filter werden hier noch die Boucherot-Schaltung als Resonanztrafo und das Collins-Filter zur Leistungsanpassung beschrieben.
Elektronische Filterschaltungen beeinflussen den Frequenzbereich zugeführter elektrischer Eingangssignale. Ein elektrisches Filter hat mindestens einen charakteristischen Durchlass- und Sperrbereich. Für den Bereichsübergang ist eine Grenzfrequenz definiert bei der die Amplitude des Ausgangssignals um a = 3 dB gedämpft ist. Das logarithmische Maß besagt, dass die Ausgangsamplitude um den Faktor 1 / √2 = 0,7071 kleiner als die Eingangsamplitude ist und einer Verstärkung von V = −3 dB entspricht. Die Filtercharakteristik kann als Dämpfungs- oder Durchlassverhalten beschrieben werden, die zueinander reziprok sind. Das Übertragungsverhalten wird fast immer als Verhältnis der Ausgangs- zur Eingangsgröße angegeben. Bei passiven Filterschaltungen ist die Ausgangsamplitude immer kleiner oder gleich der Eingangsamplitude.
Einfache Filter, zu denen RC- und RL-Tief- und Hochpässe zählen, haben nur eine Grenzfrequenz fg.
Bei fg gilt: Ua / Ue = 1 / √2 = 0,7071.
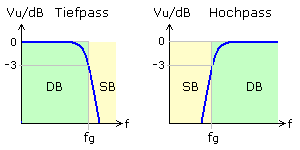
Filtergruppen
Tiefpassfilter (low pass filter)
Alle Frequenzen bis zur Grenzfrequenz (englisch cutoff frequency), teilweise als Eckfrequenz bezeichnet, werden fast ohne Abschwächung zum Ausgang durchgelassen. Die Signalamplituden der höheren Frequenzen werden zunehmend gedämpft.
Hochpassfilter (high pass filter)
Die Frequenzen oberhalb der Grenzfrequenz durchlaufen das Filter und stehen am Filterausgang ungeschwächt zur Verfügung. Je weiter man von der Eckfrequenz in den Bereich tieferer Frequenzen kommt, desto mehr werden die Amplituden geschwächt. Gleichspannungsanteile werden vollkommen gesperrt.
Bandpassfilter (band pass filter)
Zusammengesetzte Filterschaltungen mit Resonanzkreisen oder voneinander unabhängigen RC- und RL-Gruppen bilden Bandpässe oder Bandsperren. Diese Filter haben ihren charakteristischen Extremwert bei der Mittenfrequenz fo. Zusätzlich zur Mittenfrequenz gibt es an den 3 dB-Punkten eine untere fgu und obere fgo Grenzfrequenz. Die Mittenfrequenz errechnet sich als geometrischer Mittelwert aus den Grenzfrequenzen. \({f_o} = \sqrt {{f_{gu}} \cdot {f_{go}}} \). Eine weitere charakteristische Filtergröße ist die Bandbreite B, der Differenzwert zwischen der oberen und unteren Grenzfrequenz. \(B = {f_{go}} - {f_{gu}}\). Dargestellt sind prinzipielle Filterkurven mit Durchlass- DB und Sperrbereich SB und die Lage der Grenzfrequenzen.
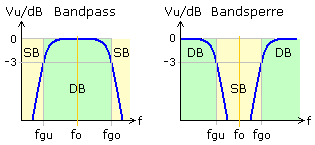
In der digitalen Audiotechnik kommt ein nach der Audio Engineering Society standardisiertes Messbandfilter AES17-1998 zum Einsatz. Es ist ein Bandpassfilter, das im Bereich von 10 Hz bis 20 kHz eine Amplitudenkonstanz von ±0,1 dB und bei 24 kHz eine Dämpfung von mindestens 60 dB aufweist.
Wird der Amplituden-Frequenzgang vom Bandpass- oder Bandsperrfilter mit linear geteilter Amplitudenachse dargestellt, dann ähnelt die Durchlasskurve dem Profil einer Glockenkurve. Die Filter werden daher auch Glockenfilter (englisch peak filter) genannt, zu denen auch Reihen- und Parallelschwingkreise zählen.
Oktavfilter und Terzfilter
Es handelt sich um Bandpassfilter, deren Grenzfrequenzen in einem festen Verhältnis stehen. Die Übertragungsfunktionen sind zumeist genormt und die Filter haben sehr steile Flanken. In der Audiotechnik ist die Oktave gleich einer Frequenzverdopplung. Die Bandbreite drei aufeinanderfolgender Terzfilter umfasst eine Oktave. Mit Festlegung einer Grenzfrequenz gelten für die Eckfrequenzen die folgenden Formeln. \[Oktavfilter:\quad {f_{go}} = 2\,{f_{gu}}\quad \quad Terzfilter:\quad {f_{go}} = \sqrt[3]{{2\,{f_{gu}}}}\quad \]
Bandsperrfilter (notch filter, band reject filter)
Die Bandsperre hat ein zum Bandpass gespiegeltes Verhalten. Das Filter selektiert ein bestimmtes, schmales Frequenzband. Prinzipiell handelt es sich um parallel geschaltete Hoch- und Tiefpässe. Alle Frequenzen bis zur unteren Grenzfrequenz und ab der oberen Grenzfrequenz passieren ohne Dämpfung. Der Frequenzbereich dazwischen wird zur Mittenfrequenz hin zunehmend geschwächt. Eine Bandsperre mit einem sehr schmalen Frequenzband, steilen Flanken und hoher Dämpfung wird Kerb- oder Notchfilter genannt. Handelt es sich um einen Reihenschwingkreis, so spricht man von Falle (trap filter) oder Saugkreis.
Allpassfilter
Der Amplituden-Frequenzgang des Allpassfilters zeigt im gesamten Frequenzbereich eine konstante Ausgangsamplitude. Das Filter besitzt eine Grenzfrequenz. Im Arbeitsbereich unterhalb der Grenzfrequenz ist die Signalgruppenlaufzeit unabhängig von der Frequenz. Das Ausgangssignal erfährt eine frequenzabhängige Phasenverschiebung. Das Allpassfilter arbeitet als Phasenschieber oder Laufzeitglied und gibt somit das Eingangssignal unverändert aber zeitverzögert an den Ausgang weiter. Ein Kammfilter ist die Zusammenschaltung mehrerer aufeinander abgestimmter Allpassfilter.
Wichtige Filtereigenschaften
Flankensteilheit
Die Flankensteilheit ist eine Kenngröße und ein Maß für die Änderung der Übertragungsamplitude im Sperrbereich. Da der Übergang vom Durchlass- in den Sperrbereich nicht mit einem scharfen Knick und linear erfolgt, ist die Angabe einer Bezugsfrequenz notwendig. Von der Grenzfrequenz ausreichend weit entfernt wird der in logarithmischer Teilung dargestellte Kennlinienverlauf linear. Die Flankensteilheit oder Dämpfung wird dann als Kenngröße pro Oktave, der Frequenzverdopplung oder Dekade, der Frequenz-Verzehnfachung angegeben. Filter n-ter Ordnung haben dort eine Dämpfung von n·6 dB/Oktave und n·20 dB/Dekade mit n als ganze Zahl größer null. Je höher die Ordnungszahl, desto eher kann eine störende Welligkeit im Durchlassbereich auftreten.
Selektivität – Güte
Neben den Nutzfrequenzen gelangen auch geringe Anteile unerwünschter Frequenzbereiche an den Filterausgang. Die Selektivität ist der Quotient der Ausgangsamplitude oder des Übertragungsfaktors im Durchlassbereich bei der Mittenfrequenz in Bezug zum Übertragungsfaktor ab einer vorgegebenen Störfrequenz. Filter mit geringer Bandbreite zeichnen sich durch eine hohe Filtergüte aus. Der benennungslose Gütefaktor Q errechnet sich als: \[Q = \frac{{{f_o}}}{B} = \frac{{{f_o}}}{{{f_{go}} - {f_{gu}}}}\]
Betriebsdämpfung
Bei passiven Filtern ist das Ausgangssignal immer kleiner als das Eingangssignal. Die Betriebsdämpfung ist das auf den Durchlassbereich bezogene Verhältnis der Eingangsleistung zur Ausgangsleistung. In aktiven Filterschaltungen kann das durch eine lineare Verstärkung ausgeglichen werden.
Phasenlaufzeit
Durchläuft ein Signal mit bestimmter Frequenz ein Filter oder eine elektronische Baugruppe, kann es zum zeitlichen Verzug kommen, der dann als Phasenverschiebung zwischen Eingangs- und Ausgangssignal messbar ist. Das Signal benötigt eine bestimmte Zeit, da es sich mit endlicher Geschwindigkeit vom Eingang zum Ausgang bewegt. In einem stationären System ist die Phasenlaufzeit die Zeit, die das Ausgangssignal benötigt, um den Phasenzustand des Eingangssignals zu erreichen.
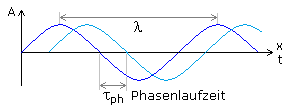
Die Phasenlaufzeit ist als Funktion der Frequenz darstellbar und wird dann mit dem Bogenmaß des Phasenwinkels berechnet. \[A(x,t) = {A_o}\,\sin \left( {2\,\pi \frac{t}{T} - \frac{{2\,\pi }}{T} \cdot \frac{{x\,T}}{\lambda }} \right)\quad \quad mit\quad k = \frac{{2\,\pi }}{\lambda }\] \[A(x,t) = {A_o}\,\sin (\omega \,t - k\,x)\] \[\varphi = \omega \,t - k\,x = konst\quad \Rightarrow x = \frac{{\omega \,t - konst}}{k}\] \[{c_{ph}} = \frac{{dx}}{{dt}} = \frac{\omega }{k} = 2\,\pi \,f\frac{\lambda }{{2\,\pi }}\] \[Phasengeschwindigkeit\quad {c_{ph}} = \lambda \cdot f\] \[Phasenlaufzeit\quad {\tau _{ph}} = \frac{x}{{\lambda \,f}}\]
Bei monofrequenten Signalen zeigt sich nur eine Phasenverschiebung und keine Verzerrung. Ist die Phasenlaufzeit eines Übertragungssystems im betrachteten Frequenzbereich konstant, dann wird das Signal verzerrungsfrei übertragen. Hoch-, Tief- und Bandpässe erfüllen im gesamten Frequenzbereich diese Phasenbedingung nicht. Signale mit vielen Oberwellen werden nicht verzerrungsfrei übertragen. Für einen RC-Tiefpass mit \(\tau = R\,C\) wird mithilfe der komplexen Übertragungsfunktion der Phasenwinkel in Abhängigkeit der Frequenz hergeleitet. \[\underline G (j\omega ) = \frac{{{{\underline U }_a}}}{{{{\underline U }_e}}} = \frac{1}{{1 + j\,\omega \,\tau }} = \frac{{1 - j\,\omega \,\tau }}{{1 + {{(\,\omega \,\tau )}^2}}}\] Für die Realkomponente (Re) und Imaginärkomponente folgen: \[{\mathop{\rm Re}\nolimits} = \frac{1}{{1 + {{(\,\omega \,\tau )}^2}}}\quad \quad {\mathop{\rm Im}\nolimits} = - j\frac{{\omega \,\tau }}{{1 + {{(\,\omega \,\tau )}^2}}}\] Damit kann der frequenzabhängige Phasenwinkel in Winkelgrad berechnet werden: \[\varphi (\omega ) = {\mathop{\rm arc}\nolimits} \,tan\left( {\frac{{{\mathop{\rm Im}\nolimits} }}{{{\mathop{\rm Re}\nolimits} }}} \right) = - {\mathop{\rm arc}\nolimits} \,tan(\omega \,\tau )\] Die Phasenlaufzeit errechnet sich mit dem negativen frequenzabhängigen Phasenwinkel im Bogenmaß dividiert durch die zugehörige Kreisfrequenz: \[{\tau _{ph}} = - \frac{{\varphi (\omega )}}{\omega }\quad mit\quad \varphi (\omega ) = \frac{{\pi \cdot \varphi (\omega )}}{{180}}\]
An einen RC-Tiefpass mit R = 1 KΩ und C = 100 nF und der Grenzfrequenz fg = 1,6 kHz wird an den Eingang ein Mischsignal aus drei Sinusfrequenzen gegeben. Liegen die drei Sinusfrequenzen unterhalb der Grenzfrequenz, dann ist nur eine geringe Phasenverschiebung messbar und das Ausgangssignals zeigt praktisch keine Verzerrungen. Durchläuft das Mischsignal mit den zehnfach höheren Einzelfrequenzen dieses Filter, dann ist das Ausgangssignal deutlich verzerrt und die Phasenlaufzeiten sind nicht mehr konstant.
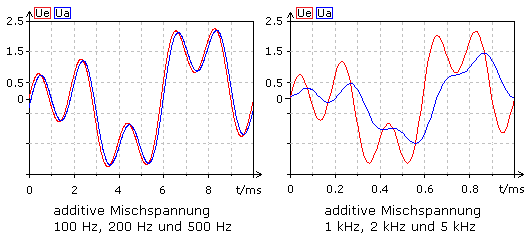
Die Abhängigkeit der Phasenlaufzeit von der Frequenz wird als Phasenverzerrung bezeichnet. Für phasenverzerrte Audiosignale ist das menschliche Ohr sehr unempfindlich. In der Farbfernsehtechnik machen sich Phasenverzerrungen als Farbtonänderungen bemerkbar, für die menschliche Augen sehr empfindlich sind.
Gruppenlaufzeit
Durchläuft eine schmalbandige Signalgruppe, beispielsweise eine Amplitudenmodulation ein Filter oder eine elektronische Baugruppe, so kommt das Signal zeitverzögert am Ausgang an. Die Gruppenlaufzeit ist die Zeit, mit der die Hüllkurve des Gesamtsignals verzögert am Ausgang erscheint. Die Gruppenlaufzeit errechnet sich aus der Ableitung des Phasengangs bei der jeweiligen Frequenz und gibt die Steigung des Phasengangs an. In einem Frequenzbereich mit linearem Phasengang sind die Gruppenlaufzeiten konstant. Ein schmalbandiges Signal, das diesen Frequenzbereich des Systems (Bandfilter) nicht überschreitet, wird unverzerrt übertragen.
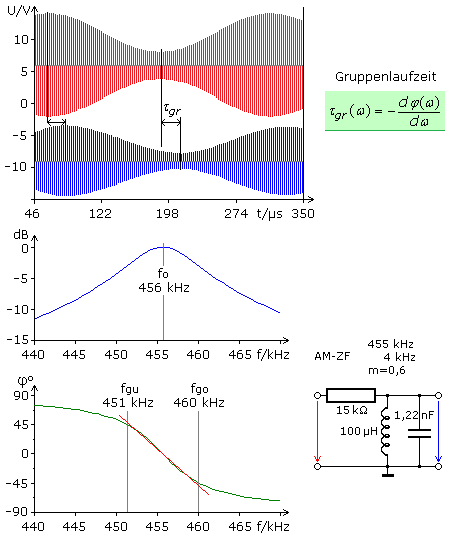
Das Bild zeigt ein einfaches Schwingkreisfilter für ein amplitudenmoduliertes Zwischenfrequenzsignal der analogen Rundfunktechnik. Die verwendete ZF-Frequenz beträgt 455 kHz und die Bandbreite des AM-Signals ist auf 9 kHz festgelegt. Der Schwingkreis hat eine Bandbreite von 11 kHz und zeigt im Bodediagramm zwischen den Grenzfrequenzen einen weitgehend linearen Phasengang. In diesem Bereich sind die Steigung der rot eingezeichneten Geraden und somit auch die Gruppenlaufzeit konstant. Das AM-ZF-Signal erscheint verzögert und unverzerrt am Filterausgang.
Die Gruppengeschwindigkeit auf Leitungen liegt zwischen 10000 km/s bis fast Lichtgeschwindigkeit. Bei Funkverbindungen über Satellit sind daher einige Sekunden Verzögerung bemerkbar. Im terrestrischen Fernmeldenetz sind Laufzeiten bis 250 ms in jeder Übertragungsrichtung zugelassen. Die dabei auftretenden Störungen des Gesprächsflusses bleiben unter 10%. Durch die frequenzabhängige Gruppenlaufzeit kommt es zu Gruppenlaufzeitverzerrungen. Sie werden auf eine feste Bezugsfrequenz oder eine Frequenz mit kleinerer Gruppenlaufzeit bezogen. Die Verzerrungen könnten im Audiobereich einzelne Sprachlaute verfälschen, da höhere Sprachfrequenzen vor den tieferen am Empfänger eintreffen. Im Audiobereich sind diese Störungen sind fast immer vernachlässigbar. In der Bildübertragung müssen sie durch besondere Maßnahmen kompensiert werden.
△Passive RC- und RL-Filter
Passive Bandpass- und Bandsperrfilter
Zu den einfachsten Grundschaltungen gehören die RC- und RL-Spannungsteiler. Diese Hoch- und Tiefpässe besitzen ein von der Frequenz abhängiges Bauteil und sind somit Pässe oder Filter 1. Ordnung. Die Reihenschaltung aus HP und TP ergibt einen Bandpass, wenn die Grenzfrequenz des TP gleich oder größer als die des HP ist. Eine abgewandelte Parallelschaltung von HP und TP führt zur Bandsperre. Die Filtereigenschaften sind nicht so gut, da sie als Filterpässe 1. Ordnung nur die Flankensteilheit von 20 dB pro Dekade oder 6 dB pro Oktave erreichen. Nachteile entstehen durch die gegenseitige Belastung bei der direkten Zusammenschaltung der Einzelpässe zum Filter. Ein zu hoher Innenwiderstand der Eingangssignalquelle und eine Ausgangsbelastung wirken sich zusätzlich negativ auf den Maximalpegel aus und verschieben die Grenzfrequenzen.
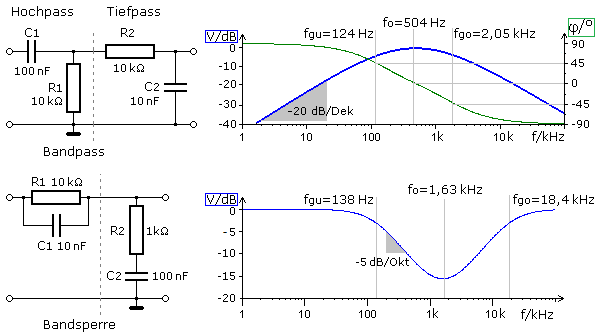
Im Bandpass beträgt die Grenzfrequenz für den Hochpass 159 Hz und für den Tiefpass 1,592 kHz. Aus dem Bodediagramm der Schaltungssimulation kann für die Mittenfrequenz fo = 504 Hz abgelesen werden. Sie errechnet sich auch als geometrisches Mittel aus den unbelasteten Grenzfrequenzen vom HP und TP. \({f_g} = \sqrt {{f_{gu}} \cdot {f_{go}}} = \sqrt {159 \cdot 1592} = 503,12\,Hz\) Wegen der gegenseitigen Belastung ergeben sich für den Bandpass andere Grenzfrequenzwerte, deren geometrisches Mittel wieder die gleiche Mittenfrequenz ergibt.
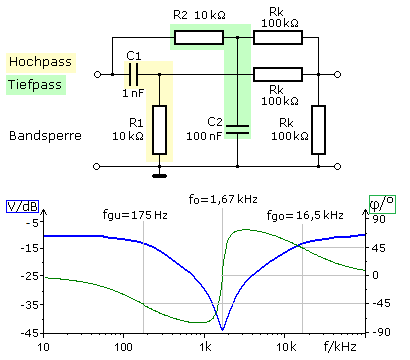
Bei einer Bandsperre sollte die Grenzfrequenz des TP kleiner als die des HP sein. Optimaler wäre eine echte Parallelschaltung beider Pässe wie in der folgenden Schaltung. Die beiden Ausgangsspannungen werden hochohmig mithilfe einer Addierstufe zum gemeinsamen Filterausgang zusammengeführt. Die Flankensteilheit ist größer, erreicht aber nicht die 12 dB/Oktave eines Filters 2. Ordnung. Die Grenzfrequenz des HP beträgt 15,92 kHz und die des TP 159 Hz und weicht in diesem Bandsperrfilter infolge der besseren Entkopplung weniger stark ab. Eine optimale Entkopplung der einzelnen Pässe ist durch nicht invertierende Operationsverstärker zu erreichen. An anderer Stelle wird der belastete RC-Bandpass mathematisch ausführlich beschrieben.
 △
△
Klangeinstellnetzwerk – Shelving Filter
Zur Klangbeeinflussung werden im Audiobereich der Heimelektronik Höhen- und Tiefeneinsteller verwendet. Im einfachsten Fall sind es passive RC-Schaltungen, die mit Potenziometern die Amplitudenfrequenzgänge beeinflusst werden. Liegen die Filter im Rückkoppelzweig zwischen zwei Verstärkerstufen, kann der einstellbare Frequenzbereich zusätzlich kontrolliert gedämpft oder verstärkt werden. Die folgende Schaltung zeigt ein passives universelles Fächernetzwerk mit einem Höhen- und Tiefeneinsteller, auch Kuh- oder Schwalbenschwanzentzerrer genannt. Es ist ein industriell verwendeter Schaltungsauszug, der dem klassischen Fächerentzerrer ähnlich ist. Hier wirken von der Frequenz abhängige Brückenzweige als einstellbare Hoch- und Tiefpässe. Das Diagramm zeigt den Amplituden-Frequenzgang für unterschiedliche Einstellungen der Höhen- und Tiefenpotis. Beim Tiefpass (TP) wird das Nutzsignal parallel zum Kondensator, beim Hochpass (HP) parallel zum Wirkwiderstand abgegriffen. Der linke Brückenzweig wirkt als TP, der rechte Brückenzweig als HP.
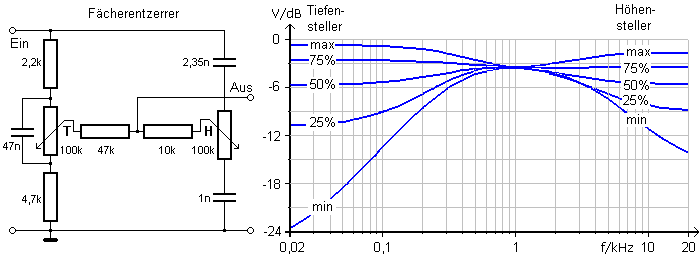
Steht der Schleifer des Tiefenstellers T oben (maximal), so bildet im linken Zweig der obere Widerstand mit dem Kondensator einen Tiefpass. Für niedrige Signalfrequenzen hat der Kondensator einen hohen Widerstandswert. Bei 100 Hz sind es rund 33 kΩ, bei 1 kHz sind es 3,4 kΩ. In der Parallelschaltung bestimmt der Kondensator den wirksamen Teilwiderstand und abhängig von der Schleiferstellung wird mehr oder weniger Signalamplitude über den Brückenzweig zum Ausgang ausgekoppelt. In der unteren Position (minimal) koppelt der Tiefensteller die Signalamplitude am unteren Widerstand aus. Mit diesem Widerstand bildet der 47 nF Kondensator einen RC-HP. Die hohen Frequenzanteile im Eingangssignals werden von diesem Kondensator kaum gedämpft und stehen als relativ große Signalamplitude am unteren Widerstand zur Verfügung. Der linke Brückenzweig wirkt mit dem Poti auf die tiefen Signalfrequenzen.
Steht im rechten Brückenteil der Schleifer des Höhenstellers H oben (maximal), so bildet er mit dem oberen Kondensator einen Hochpass. Die im Eingangssignal vorhandenen niederfrequenten Signalanteile werden vom oberen Kondensator stark gedämpft, während die höheren Frequenzen am Bahnwiderstand des Potis eine hohe Signalamplitude haben. Bei einer Frequenz von 1 kHz hat der obere Kondensator einen Widerstandswert von rund 68 kΩ und bei 5 kHz sind es rund 13,5 kΩ. Die höheren Signalfrequenz werden vom Kondensator immer weniger gedämpft und die vom Schleifer abnehmbare Signalamplitude nimmt bei unveränderter Stellung zu. Je nach Schleiferstellung wird eine mehr oder weniger große Signalamplitude zum Ausgang ausgekoppelt. Der rechte Brückenzweig dämpft die im Eingangssignal vorhandenen höheren Signalanteile nur wenig. In der unteren Schleiferposition (minimal) wird das Signal am unteren Kondensator ausgekoppelt und der Höhensteller bildet mit diesem Kondensator einen Tiefpass. In dieser Stellung sind im ausgekoppelten Signal die hohen Frequenzbereiche am stärksten gedämpft.
Keine der beiden Brückenseiten sind reine Hoch- oder Tiefpässe. Je nach Schleiferstellung sind beide Eigenschaften mehr oder weniger wirksam. Eine einfache Grenzfrequenzberechnung ist hier nicht möglich.
△T- und Pi-Filterschaltung
Beim Zusammenschalten von zwei gleichen Pässen gibt es zwei Schaltungsvarianten, die ihrem Aussehen nach den Buchstaben T oder Pi bilden. Bei RC- und RL-Pässen sind beide Schaltungsvarianten gleichwertig. Im unteren und mittleren Frequenzbereich werden nach Möglichkeit RC-Filter bevorzugt, da Spulen teurer, größer und im Vergleich zu Kondensatoren eine geringere Güte haben. T- und Pi-Filterschaltungen in LC-Technik bilden Filter höherer Ordnung mit steileren Flanken und einer besseren Trennung zwischen Durchlass- und Sperrbereich. Das Bild zeigt einige einfache Grundtypen.
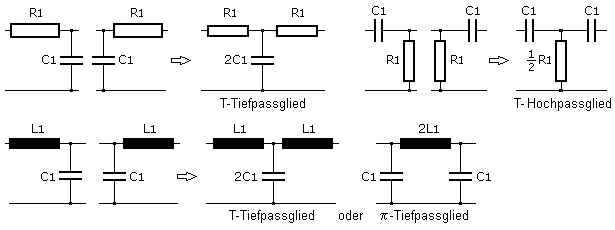
Die folgende Schaltung zeigt die Anwendung eines Pi-Filters. Es handelt sich um ein Präsenzfilter zur Verbesserung der Sprachverständlichkeit. Die Schaltung wurde in einem Hi-Fi-Empfänger der Firma SABA eingesetzt. Entsprechend der Telefonie Bandbreite liegt das Sprachband zwischen 300 Hz bis 3,4 kHz. Dieses Filter arbeitet zwischen 1,2 kHz ... 5,5 kHz mit dem Durchgangsmaximum bei einer Mittenfrequenz von 2,6 kHz. Im Empfänger befindet sich das Filter im Rückkopplungszweig zweier Transistoren, wodurch die Dämpfung in eine Verstärkung umgekehrt wird. Vom Ausgang betrachtet wirkt der 22 nF Kondensator in der Brückenverbindung mit dem 5,6 kΩ als Hochpass auf den Eingang zurück. Vom Eingang her gesehen stellt dieser Kondensator mit dem 1,8 kΩ einen Hochpass dar. Mit ihm verliert der Tiefpass im Ausgangszweig zu höheren Frequenzen seinen Einfluss.
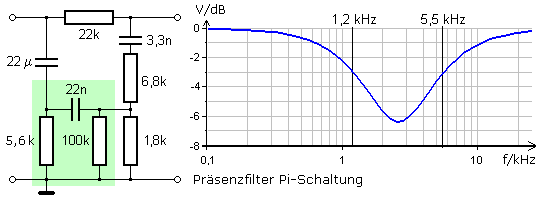
Ein weiteres Beispiel zeigt die Anwendung eines Doppel-T- oder Kerbfilters aus RC-Hoch- und Tiefpassgliedern. Es handelt sich um eine 16 kHz Sperre zum Abblocken des Gebührenimpulses im Telefonverkehr, der den Modembetrieb am PC stören konnte. Die per Simulation ermittelte Mittenfrequenz liegt bei 15,8 kHz. Bei gleichen Widerstands- und Kondensatorwerten im Durchgangszweig hat der nach Masse geschaltete Widerstand den halben Wert und der Kondensator den doppelten Wert.
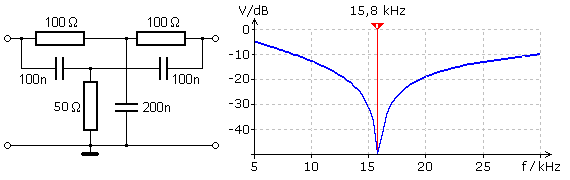
Fernspeiseweiche (bias tee)
Die Fernspeiseweiche, ein in der HF-Technik T-förmig aufgebautes Filter, trennt eine DC-Versorgungs- oder Schaltspannung von HF-Signalen. Es sind Frequenzweichen, die im engl. Sprachgebiet als bias tee bezeichnet werden und oft in der Antennentechnik vor HF-Verstärkern und Vorverstärkern eingesetzt werden. In der oberen Schaltung kann die DC-Versorgungsspannung nicht über den Kondensator C1 an den HF-Ausgang gelangen. Der hohe induktive Widerstand sperrt die HF nach unten hin, ist aber für DC und niedrige Frequenzen unwirksam. Die Gleichspannung wird zwischen C2 und L ein- oder ausgekoppelt und ist durch C2 von der Masse getrennt, während restliche HF-Anteile nach Masse kurzgeschlossen werden.
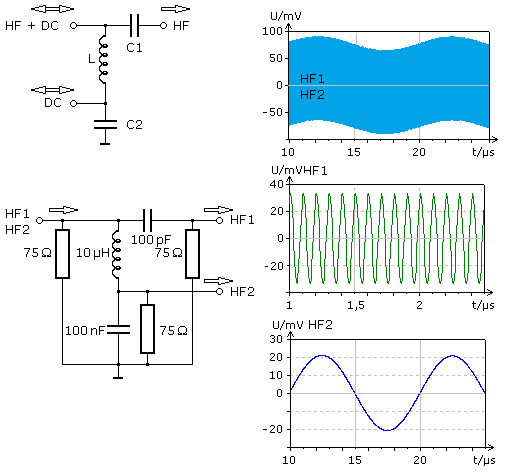
Bei geeigneter Dimensionierung der Bauteile kann diese Weiche auf gleichem Weg auch ein gemischtes HF-Eingangssignal trennen. Die zweite Schaltung zeigt die mithilfe einer Simulation erstellte Funktionsweise. Zum einfachen Ausfiltern ist der Abstand der HF1-Frequenz mit 10 MHz weit genug entfernt von der HF2-Frequenz mit 100 kHz. Als Ein- und Ausgangswiderstände werden die in der Antennentechnik gebräuchlichen 75 Ω eingesetzt.
△Filter höherer Ordnung – passive LC-Filter
Die bisher vorgestellten Filter haben keine steilen Flanken. Mit nur einem von der Frequenz abhängigen Bauteil weisen die Grundglieder eine maximale Flankensteilheit von 6 dB pro Oktave oder 20 dB pro Dekade auf. LC-Filter mit zwei von der Frequenz bestimmten Bauteilen zeigen mit 12 dB pro Oktave oder 40 dB pro Dekade eine bessere Filterwirkung. Ohne zusätzliche Wirkwiderstände ist die Grunddämpfung im Durchlassbereich viel geringer. Neben diesen Vorteilen kann das Resonanzverhalten der einfachen LC-Glieder problematisch sein. Die Filter müssen, wie bei den Lautsprecherweichen gezeigt, auf den angeschlossenen Lastwiderstand angepasst werden.
Eine Spule und ein Kondensator in Reihe geschaltet bildet einen Reihenschwingkreis mit einer Resonanzfrequenz und zwei Grenzfrequenzen. Der Amplitudenverlauf des Ausgangssignals, das parallel zum Kondensator abgegriffen wird, nimmt nach der oberen Grenzfrequenz ab. Diese Schaltungsvariante ist mit einem Tiefpass vergleichbar. Zwischen den Grenzfrequenzen liegt die Resonanzfrequenz, die mithilfe der Thomson-Formel berechnet werden kann und zur Filterfrequenz wird. Am Blindwiderstand entsteht eine Spannungsüberhöhung, die von der Kreisgüte abhängig ist. Nimmt man für L und C ideales Verhalten an, wird die Kreisgüte durch den Quelleninnenwiderstand und durch den Lastwiderstand bestimmt. Mit einer angepassten Belastung wird die Überhöhung vermieden und die Flankensteilheit bleibt für das Filter 2. Ordnung bestehen.
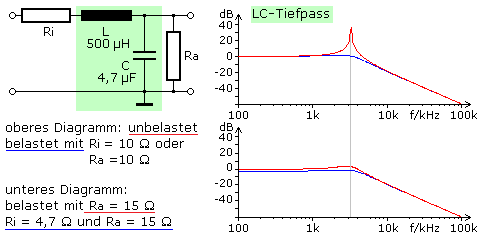
Werden in der Schaltung die Plätze von L und C getauscht und das Ausgangssignal parallel zur Spule abgegriffen, dann ist der Frequenzbereich bis zur Grenzfrequenz stark gedämpft und die Schaltung wirkt als Hochpass. Die Amplitudendiagramme sind für die gleichen Belastungsfälle spiegelsymmetrisch zur Mitten-(Resonanz)frequenz.
Ein LC-Parallelschwingkreis zeichnet sich bei Resonanzfrequenz durch Spannungsüberhöhung und starker Dämpfung außerhalb des Bandbreitenbereichs aus. Die Bandbreite ist von der Belastung durch die Quellenimpedanz und die Lastimpedanz der Folgestufe bestimmt. Die Güte der Spule ist vom Drahtwiderstand bestimmt und meistens wesentlich höher. Mit zunehmender Belastung wird die Bandbreite B größer und die Filtergüte Q geringer. Sie errechnet sich mit Q = fo / B, aus dem Verhältnis der Mittenfrequenz zur Bandbreite. Mit abnehmender Güte wird auch die Flankensteilheit deutlich kleiner.
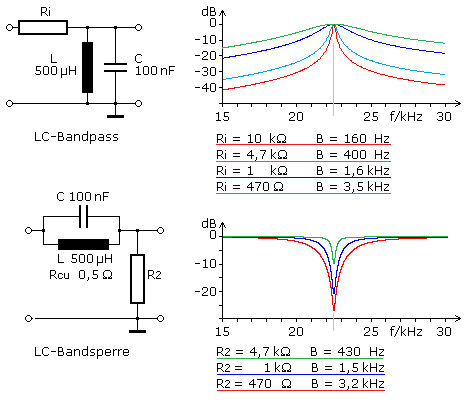
Liegt der Schwingkreis in Serie zum Signalweg, so entsteht eine Bandsperre. Die Kreisgüte ist in der Simulation durch den eingefügten Drahtwiderstand der Spule auf Q = 140 bestimmt. Ein kleinerer Ausgangswiderstand belastet das Filter stärker, sodass die Güte abnimmt und die Bandbreite zunimmt. Gleichzeitig nimmt die Flankensteilheit im Übergangsbereich vom Durchlass in den Sperrbereich ab.
Bessere Eigenschaften ergeben sich beim Einsatz von T- und Pi-Filtergliedern. Die Grundbausteine der LC-Filterschaltungen werden Halbglieder genannt. Sie bilden einen auf den Eingang bezogenen Längspol und vom Ausgangs gesehenen Querzweipol. Das Produkt aus Längs- und Querimpedanz sollte frequenzunabhängig sein. Die später folgenden Bilder zeigen die vier wichtigsten Grundhalbglieder. Eine Spule im Längszweig führt ebenso wie der Kondensator im Querzweig zum Tiefpass. Für einen Hochpass liegt der Kondensator im Längszweig und die Spule im Querzweig. Ebenso ergänzen sich in einem Bandpass ein Reihenschwingkreis längs vom Eingang mit einem Parallelschwingkreis quer zum Ausgang geschaltet. Werden die Schwingkreise gegeneinander ausgetauscht, so entsteht eine Bandsperre.
Dualität in elektronischen Schaltungen
Zwei unterschiedliche Schaltungen, Schaltelemente oder Baugruppen verhalten sich dual zueinander wenn die Beziehung zwischen Spannung und Strom der einen Schaltung der Beziehung zwischen Strom und Spannung der anderen Schaltung zu den gleichen Eigenschaften führt. Duale Baugruppen können Spannungs- und Stromquellen sowie Wirkwiderstände und ihre Leitwerte und (ideal angenommene) Blindelemente sein. In dualen Schaltungen sind die Quellen als auch die Schaltelemente gegeneinander getauscht. Eine duale Spannungsquelle wird durch eine duale Stromquelle getauscht. Eine Baugruppe mit dem Widerstand R kann direkt durch eine Baugruppe mit dem Leitwert des reziproken Widerstands ersetzt werden. Wird eine Spannungsquelle durch eine Stromquelle oder Stromquelle durch eine Spannungsquelle ersetzt, dann soll bespielsweise die gleiche Leistung übertragen werden. Es gelten die allgemeinen Beziehungen mit den Proportionalitätswerten k1 und k2: \[{u_{dual}} = {k_1} \cdot i\quad {i_{dual}} = {k_2} \cdot u\] \[P = u \cdot i = {u_{dual}} \cdot {i_{dual}}\quad \to {k_1} \cdot {k_2} = 1\] Eine der Variablen k wird als Dualitätsinvariante Ro manchmal auch als Z bezeichnet. Invarianz bezeichnet in der Mathematik die Unveränderlichkeit einer Größe. Wird in einer Schaltung k1 als Dualitätsinvariante definiert, dann ist k2 als Kehrwert abhängig. \[{k_1} = {R_o}\quad \to {k_2} = \frac{1}{{{R_o}}}\] In die allgemeinen Gleichungen mit k1 = Ro eingesetzt folgt für duale Spannungs- und Stromquellen: \[{u_{dual}} = {k_1} \cdot i\quad \to {u_{dual}} = {R_o} \cdot i\quad und\quad i = \frac{1}{{{R_o}}} \cdot {u_{dual}}\] \[{i_{dual}} = {k_2} \cdot u\quad \to {i_{dual}} = \frac{1}{{{R_o}}} \cdot u\quad und\quad u = {R_o} \cdot {i_{dual}}\quad \] Für die Widerstände R und und ihre Leitwerte G gilt schrittweise hergeleitet: \[R = \frac{u}{i} = \frac{{{R_o} \cdot {i_{dual}}}}{{\frac{1}{{{R_o}}} \cdot {u_{dual}}}} = R_o^2 \cdot \frac{{{i_{dual}}}}{{{u_{dual}}}} = R_o^2 \cdot {G_{dual}}\] \[G = \frac{i}{u} = \frac{{\frac{1}{{{R_o}}} \cdot {u_{dual}}}}{{{R_o} \cdot {i_{dual}}}} = \frac{1}{{R_o^2}} \cdot \frac{{{u_{dual}}}}{{{i_{dual}}}} = \frac{1}{{R_o^2}} \cdot {R_{dual}}\] Werden die Blindkomponenten L und C getauscht, so muss für das duale Verhalten gleichzeitig u gegen i getauscht werden: \[u = L \cdot \frac{{d\,i}}{{d\,t}}\quad und\quad i = C \cdot \frac{{du}}{{dt}}\] \[L = \frac{u}{{\frac{{di}}{{dt}}}} = \frac{{{R_o}}}{{\frac{1}{{{R_o}}}}} \cdot \frac{{{i_{dual}}}}{{\frac{{d{u_{dual}}}}{{dt}}}} = R_o^2 \cdot {C_{dual}}\] \[C = \frac{i}{{\frac{{du}}{{dt}}}} = \frac{{\frac{1}{{{R_o}}}}}{{{R_o}}} \cdot \frac{{{u_{dual}}}}{{\frac{{d{i_{dual}}}}{{dt}}}} = \frac{1}{{R_o^2}}{L_{dual}}\] Die Herleitungen gelten für den Zeitbereich und auch für sinusförmige Eingangsgrößen.
△Grundhalbglieder passiver LC-Filterschaltungen
Die folgenden Betrachtungen beschreiben Filterschaltungen, die mithilfe von LC-Halbgliedern aufgebaut sind und sich dual verhalten sollen. Die wichtigsten Gleichungen sind dem Buch von D. Stoll: Einführung in die Nachrichtentechnik, AEG-Telefunken 1979 entnommen. Jedes Halbglied hat einen Längszweipol und Querzweipol mit den (idealen) komplexen Impedanzen \(j\,{X_{lang}}\) und \(j\,{X_{quer}}\).
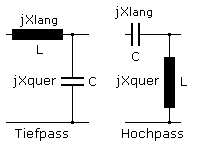
Bei der Multiplikation der komplexen Gleichungen für XL und XC steht Z steht für die Dualitätsinvariante Ro. Das Produkt beider Impedanzen ist von der Frequenz unabgängig: \[{Z^2} = j\,\omega \,L \cdot \frac{1}{{j\,\omega \,C}} = \frac{L}{C}\quad mit\quad Z = {R_o} = \sqrt {\frac{L}{C}} \] Für die Grenzfrequenz fo beider Pässe gilt: \[{f_o} = \frac{1}{{2\,\pi \,\sqrt {L\,C} }}\] Die Bauteildimensionierung für die gleiche Grenzfrequenz
Die Berechnung von Bandpass und Bandsperre ist anspruchsvoller. Eine Schaltung mit einem Reihenschwingkreis als Längskomponente und einem Parallelschwingkreis als Querkomponente funktioniert als Bandpass. Werden die Schwingkreise gegeneinander ausgetauscht, entsteht eine Bandsperre. Für die Grundglieder Hoch- und Tiefpass werden folgende Formeln angegeben:
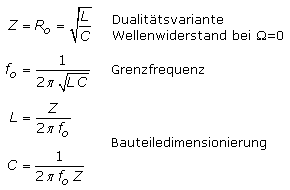
Für das Grundhalbglied LC-Bandpass gelten die Bestimmungsgleichungen:
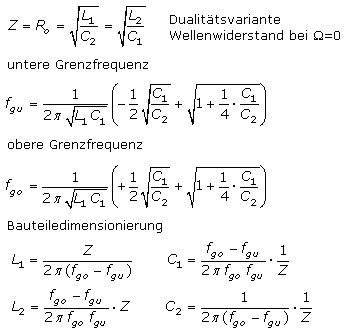
Für das Grundhalbglied LC-Bandsperre gelten die Bestimmungsgleichungen:
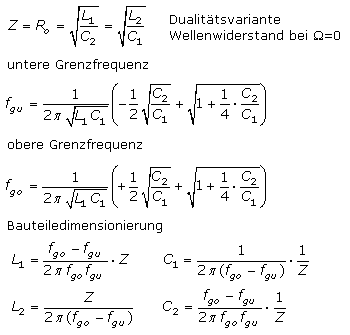
Resonanztrafo – Boucherot-Schaltung
Ein LC-Filterhalbglied als Serienschwingkreis in Resonanz mit einem zum Kondensator parallel geschalteten Lastwiderstand betrieben, wird als Boucherot-Schaltung bezeichnet. Durch den Lastwiderstand fließt bei Resonanz ein konstanter Strom, und da die Schaltung wie ein Transformator Spannung, Strom und Leistung übertragen kann, wird sie auch als Resonanztrafo bezeichnet. Sie dient unter anderem der Leistungsanpassung zwischen dem Innenwiderstand einer Quelle und der angeschlossenen Last.
Das Verhalten der Schaltung wurde mit einem Simulationsprogramm untersucht. Die Versuchsparameter sind eine Induktivität L = 800 mH mit \({Z_1} = j\,\omega \,L\), und eine Kapazität C = 12,5 μF mit \({Z_2} = \frac{1}{{j\,\omega \,C}}\). Die Resonanzfrequenz beträgt 50 Hz. Als effektive Eingangsspannung wurden 10 V gewählt. Für den Lastwiderstand Z3 wird zur einfacheren Herleitung ein Wirkwiderstand gewählt. Mit der Gesamtimpedanz kann der Eingangsstrom berechnet werden, der in gleicher Größe durch die Ausgangsimpedanz, der Parallelschaltung Z2 mit Z3 fließt. \[{I_{ges}} = \frac{{{U_e}}}{{{Z_1} + ({Z_2}||{Z_{Last}})}} = \frac{{{U_{Last}}}}{{{Z_2}||{Z_{Last}}}}\] Für die Parallelschaltung gilt: \({U_{Last}} = {Z_{Last}} \cdot {I_{Last}}\), sodass mit den folgenden Schritten der Laststrom berechnet werden kann: \[{I_{Last}} = \frac{{{U_e}({Z_2}||{Z_{Last}})}}{{{Z_{Last}}[{Z_1} + ({Z_2}||{Z_{Last}})]}}\] \[{I_{Last}} = \frac{{{U_e}}}{{\frac{{{Z_{Last}} \cdot {Z_1}}}{{{Z_2}||{Z_{Last}}}} + {Z_{Last}}}}\quad mit\quad {Z_2}||{Z_{Last}} = \frac{{{Z_2}\,{Z_{Last}}}}{{{Z_2} + {Z_{Last}}}}\] \[{I_{Last}} = \frac{{{U_e}\,{Z_2}}}{{{Z_1}\,{Z_2} + ({Z_1} + {Z_2})\,{Z_{Last}}}}\] Bei der vorausgesetzten Resonanz gilt für die absoluten Impedanzwerte
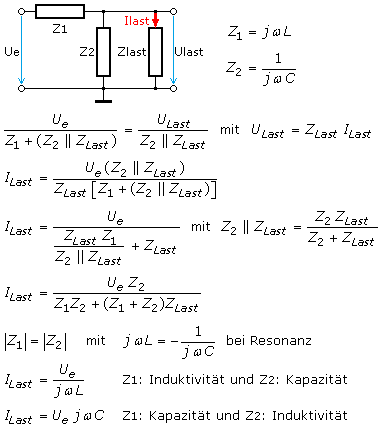
Untersucht wurde eine Simulationsschaltung mit Z1 als Induktivität L = 800 mH, und der Kapazität Z2 zu C = 12,5 μF bei der Resonanzfrequenz von 50 Hz. Bei einer konstanten sinusförmigen effektiven Eingangsspannung von 10 V wurden für unterschiedliche Lastwiderstände Ra die Eingangsströme Ie, Lastströme Ia und Spannungen Ua an der Last ermittelt. Die Tabelle zeigt den mathematisch vorhergesagten konstanten Laststrom.
| Ra / kΩ | 0,1 | 0,5 | 1 | 2 | 5 | 10 |
|---|---|---|---|---|---|---|
| Ie / mA | 42,8 | 87,6 | 161 | 313 | 757 | 1400 |
| Ua / V | 3,98 | 19,9 | 39,8 | 79 | 192,5 | 354 |
| Ia / mA | 39,8 | 39,8 | 39,75 | 39,6 | 38,5 | 35,4 |
Schaltungen mit dem Resonanztrafo finden man in der Ansteuerung von Energiesparlampen und elektronisch gesteuerten Leuchtstoffröhren sowie dem Betrieb der CCFL-Kaltkathodenröhren für die Hintergrundbeleuchtung von TFT-LCD-Flachbildschirmen. Solange eine Leuchtstoffröhre nicht gezündet hat, ist ihr Lastwiderstand sehr hoch und der Resonanztrafo stellt dann, wie aus den Tabellenwerten zu ersehen, selbst die notwendig hohe Zündspannung bereit.
In der Hochfrequenztechnik und in Sende- und Empfangsgeräten kann mithilfe von Resonanztransformatoren Leistungsanpassung zwischen unterschiedlichen Funktionsblöcken erreicht werden. Die Impedanz der Quelle, im folgenden Beispiel auf ihren Innenwiderstand R1 vereinfacht, liegt parallel zur LC-Reihenschaltung. Die Lastimpedanz, vereinfacht auf einen Widerstand R2 liegt parallel zum Kondensator. Bei Leistungsanpassung gibt die linke Seite mit ihrem Innenwiderstand ebenso viel Leistung an die Last R2 ab, wie eine gedachte Quelle rechts mit dem Last-Innenwiderstand R2 an die linke Seite abgeben würde, wo dann R1 als Last zu sehen ist.
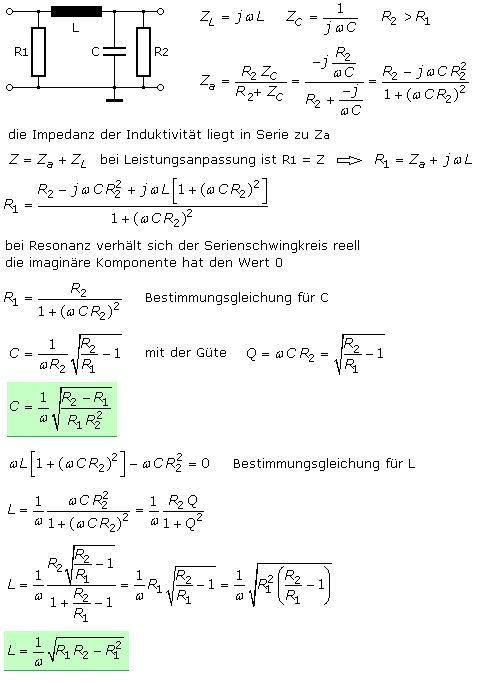
Im folgenden Beispiel wird in einer UKW-ZF-Filterkette der Ausgang eines niederomigen ZF-Quelle mit R1 = 50 Ω an eine hochohmige Folgestufe mit R1 = 2,2 kΩ mit größtmöglicher Leistung angepasst. Die Resonanzfrequenz beträgt 10,7 MHz. Mit den hergeleiteten Formeln berechnen sich die Induktivität zu 4,9 μH und die Kapazität zu 44 pF. Die Leistungswerte wurden mithilfe einer Schaltungssimulation bestimmt.
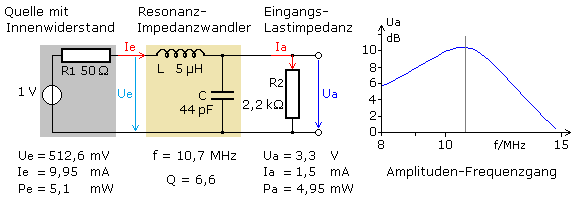
Collins-Filter
Je weniger sich die Werte der Quellen- und Lastimpedanz unterscheiden, desto geringer ist die Betriebsgüte und der Resonanztrafo hat eine große Bandbreite. Weil das LC-Filter die Impedanzen in beiden Richtungen transformieren kann, lassen sich zwei unterschiedlich dimensionierte LC-Tiefpässe zu einem PI-Filter zusammenschalten. Die Anordnung wird PI-Koppler oder nach der Firma Rockwell Collins als Collins-Filter bezeichnet, die sie in ihren Funkgeräten verwendete. Mit dem Filter sind Impedanzanpassungen zwischen Quelle und Last auch für höhere Gütewerte möglich. Abstimmbare Collins-Filter werden oft in der HF-Technik zur reflexionsarmen leistungsangepassten Signalübertragung zwischen Senderendstufe und Antenne eingesetzt. Bei der Betriebsfrequenz soll eine maximale Leistungsübertragung erfolgen und die Dämpfung außerhalb der Bandbreite möglichst hoch sein.
Zwei Resonanztransformatoren bilden mit den Induktivitäten in Serie geschaltet ein Collins-Pi-Filter. Die Eingangs- und Ausgangsbelastungen liegen auf das Signal bezogen parallel zu den Kondensatoren. So wird der Lastwiderstand der einen Seite auf einen gedachten kleinen Hilfswiderstand herab transformiert und dieser im zweiten Schritt auf die andere Seite zum Lastwiderstand hoch transformiert. Die Leistungsanpassung kann im Fall der Resonanz durch das Verhältnis der beiden Kondensatoren bestimmt werden.
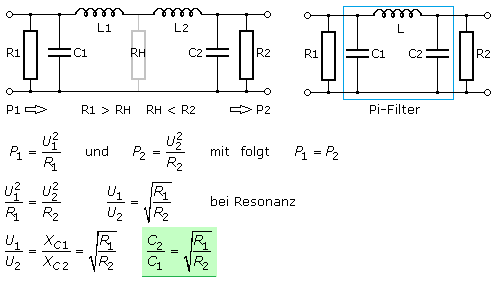
In D. Stoll: Einführung in die Nachrichtentechnik, AEG-Telefunken 1979 werden zur Leistungsanpassung mithilfe des Collins-Filters zur Dimensionierung von L und C die nachfolgenden Beziehungen angegeben. Mit diesen Gleichungen wurde eine Simulationsschaltung dimensioniert, um eine niederohmige Senderantenne an einen hochohmigen KW-Röhrensender für die Frequenz 10 MHz und einer Betriebsgüte von 15 anzupassen. Filter mit hoher Betriebsgüte haben eine große Selektivität und kleine Bandbreite aber auch größere Verluste. Normalerweise werden Werte zwischen 10 bis 20 gewählt.
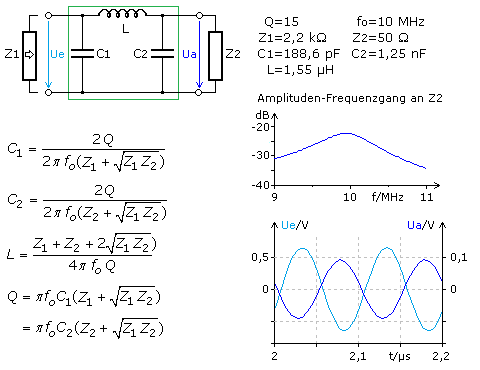
In der Sendertechnik (Amateurfunk) sind die Kondensatoren des Collins-Filters abstimmbar, zum Teil kann auch die Induktivität durch Anzapfungen umschaltbar oder als Rollenspule abstimmbar ausgeführt sein. Die optimale Feinabstimmung wird dann mit einem Stehwellenmessgerät vorgenommen. Die Simulationsschaltung bestätigt für die gewählten Lastimpedanzen das Verhältnis von C2 / C1 / = 6,63. Eine optimale Leistungsanpassung konnte mit Strom- und Spannungsmessungen bei der Simulation nicht nachgewiesen werden. Die Eingangsspannung Ue am Filter war 30% höher als sie dem gemessenen Spannungsfall am Quelleninnenwiderstand nach sein sollte.
△Eingliedrige LC-Grundketten
Zwei miteinander kombinierte Filter-Halbglieder ergeben eine eingliedrige Filterkette in T- oder PI-Schaltung. Ein für den Durchlassbetrieb optimiertes Filter wird in Leistungsanpassung betrieben. Die Anschlusswiderstände am Ein- und Ausgang sollten dem Wellenwiderstand des Filters entsprechen. Ein bekanntes Anwendungsbeispiel sind Tonfrequenzweichen. Ist nur die selektive Eigenschaft des Filters wichtig, wird es in Spannungsanpassung betrieben und möglichst wenig (hochohmig) belastet. Diese Betriebsart findet man in der Nachrichten- und Übertragungstechnik beim Bandfilter, ZF-Filter und in Selektivverstärkern. Das Bild zeigt einfache Schaltungsvarianten eingliedriger Grundketten und ihr Durchlassverhalten im Frequenzdiagramm.
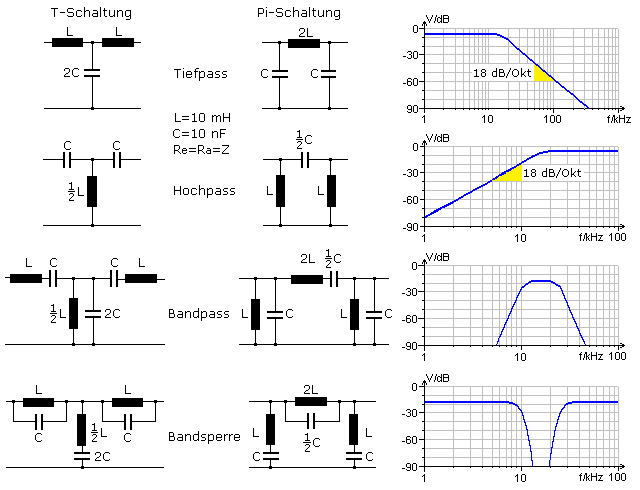
Die Durchlasskurven zeigen gute Filtereigenschaften. Es sind keine Resonanzstellen vorhanden und die Flanken der Hoch- und Tiefpässe sind mit 18 dB pro Oktave dreifach steiler als bei einfachen
RC- oder RL-Filtern. Wegen der symmetrischen Schaltung ist die Eingangs- und Ausgangsimpedanz von der Frequenz abhängig. Für Filter im Durchlassbereich wird fast immer die Leistungsanpassung gewählt. Einen noch steileren Flankenverlauf erhält man etwas außerhalb der Leistungsanpassung, wobei sich für T- und Pi-Filter unterschiedliche Koeffizienten als günstig erwiesen haben.
Für T-Filter gilt: RL = 0,8 · Z
Für Pi-Filter gilt: RL = 1,25 · Z
Im Sperrbereich ist die Eingangsimpedanz aller T-Filter sehr hoch, während sie bei den Pi-Filtern sehr klein ist. Da die Filtertechnik ein mathematisch anspruchsvolles und kompliziertes Fachgebiet ist, wird es hier nicht weiter ausgeführt. Zur Filtertechnik gibt es Spezialliteratur, die Dimensionierung kann mit Filtertabellen und Online-Rechenprogrammen aus dem Internet durchgeführt werden.
△ △
△