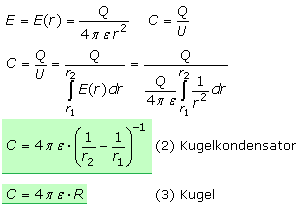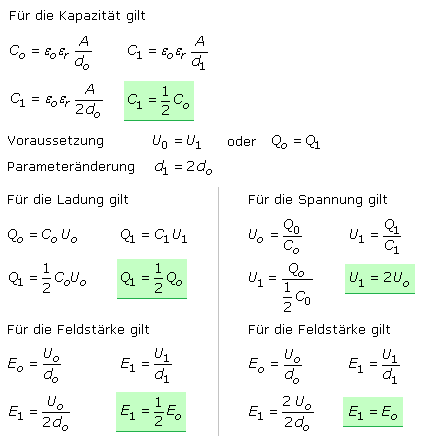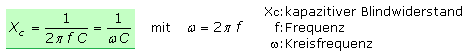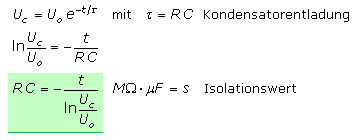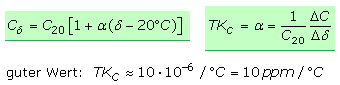Der Kondensator als elektrische Kapazität
Zwei gegeneinander elektrisch isolierte und parallel angeordnete Metallplatten werden als Plattenkondensator bezeichnet. Es ist die einfachste Bauform eines Kondensators. Wird eine Platte oder Elektrode mit dem Pluspol einer Gleichspannungsquelle und die andere mit ihrem Minuspol verbunden, bildet sich zwischen den Elektrodenbelägen ein elektrisches Feld. Wird die DC-Quelle entfernt oder der Stromkreis unterbrochen, dann bleibt das elektrische Feld zwischen den Kondensatorplatten bestehen. Parallel zum Kondensator kann die zuvor angelegte Ladespannung gemessen werden. Ein Kondensator speichert elektrische Energie.
Größere Platten- oder Elektrodenflächen können mehr Ladungen aufnehmen. Wird der Abstand der Elektroden verringert, so nimmt die Anziehungskraft zwischen den ungleichen Ladungen auf den Elektroden zu. Eine positive Ladung übt ebenso wie eine negative Ladung Kraft aufeinander aus, die zudem vom Abstand zwischen beiden Ladungen abhängig ist. Mit dem Coulomb-Gesetz wird die elektrische Feldstärke berechnet. Sie ist proportional zum Produkt der Ladungen und umgekehrt proportional Produkt der Ladungsabstände. Das elektrische Feld ist der Quotient der elektrischen Feldstärke dividiert durch die Ladung, die es erzeugt. Die Größe des Speichervermögens ist die Kapazität C des Kondensators und hat als Maßeinheit das Farad F.
Die Kapazität eines Kondensators ist die Eigenschaft unter dem Einfluss elektrischer Spannung elektrische Ladung zu speichern. Die dabei aufgenommene Ladung ist direkt proportional zur angelegten Spannung.
Beim Ladevorgang werden elektrische Ladungen verschoben. Die aufgenommene Ladung ist gleich dem Verschiebungsfluss Ψ. Die Verschiebeflussdichte D ist proportional zum elektrischen Feld E und einer Materialkonstante ε. Mit den mathematischen Zusammenhängen zum
elektrischen Feld kann die Gleichstromkapazität wie folgt hergeleitet werden.

Ein Kondensator hat die Kapazität C = 1 F, wenn bei einem Strom von 1 A innerhalb einer Sekunde
parallel zu den Anschlüssen die Spannung um 1 V zunimmt.
Die Kapazität C ist direkt proportional zur Plattengröße A.
Die Kapazität C ist umgekehrt proportional zum Plattenabstand d.
Die Kapazität C ist direkt proportional zur Eigenschaft des Dielektrikums εr.
Historische Kapazitätswerte
In sehr alten Geräten haben Kondensatoren nicht die gewohnten Kapazitätswerte nach dem SI-System in der Maßeinheit Farad. Sie ist nach dem nicht mehr gebräuchlichen CGS-System im cm-Maß angegeben.
Die Umrechnung erfolgt mit dem Faktor 1,11 pF/cm. Der Zusammenhang, dass 10 pF ≈ 9 cm entspricht, beruht auf der Kapazität
C = 4·π·ε0·R einer geladenen Kugel im Zentrum einer weit (gegen unendlich) entfernten äußeren Kugel. Es gelten die Gesetze für ein inhomogenes elektrisches Feld. Die elektrische Feldstärke E nimmt mit dem Quadrat der Entfernung ab. Ohne ausführliche Herleitung kann gezeigt werden, dass die Kapazität der Kugel im
cgs-Einheitensystem einer Strecke entspricht.
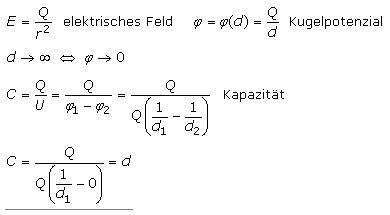
Die mathematische Herleitung der Kapazität eines Kugelkondensators führt zur Gl.(2). Eine innere Kugel ist konzentrisch von einer größeren Außenkugel umgeben. Ist diese Anordnung auf die Ladung Q aufgeladen, dann ist nur im Innenraum der umgebenen Kugel zwischen beiden Kugelflächen eine Spannung U messbar. Sie ist bei konstanter Ladung vom Abstand zu den Kugelradien abhängig. Wird bei konstanter Ladung der Radius der äußeren Kugel gegen Unendlich vergrößert, dann kann die Kapazität der Innenkugel durch Gl.(3) bestimmt werden.
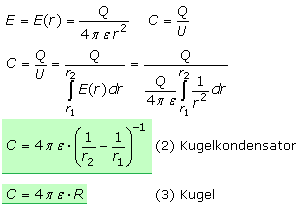
Mit dem mittleren Erdradius von 6371 km und der Annahme, dass über die weite Entfernung der äußeren Kugelschale in guter Näherung nur die Vakuum-Feldkonstante εo wirksam ist, errechnet sich die Kapazität der Erde zu rund 700 μF. Wird der Kapazitätswert durch den Radius dividiert, dann ist das Verhältnis gleich dem zuvor angegebenen Umrechnungsfaktor
1,1 pF/cm.
Spannungs- und Feldstärkeänderungen
Wird ein Plattenkondensator auf die Spannung Uo geladen, dann trägt er die Ladungsmenge Qo. Bei Vernachlässigung des inhomogenen Streufeldes an den Plattenrändern ist Eo die Feldstärke zwischen den Platten. Eine Änderung des Plattenabstands wirkt sich auf die Spannung und Feldstärke des aufgeladenen Kondensators aus. Die Ergebnisse unterscheiden sich, je nachdem ob die Spannungsquelle angeschlossen oder nach dem Aufladen abgetrennt bleibt.
Die Kapazität des Kondensators ist in beiden Fällen umgekehrt proportional zum Plattenabstand, alle anderen Parameter bleiben konstant. Die Berechnungen erfolgen mit den Formeln für die Ladung und Feldstärke. Mit angeschlossener Spannungsquelle bleibt die Spannung am Kondensator konstant. Die Landungsmenge und Feldstärke verhält sich umgekehrt proportional zum Plattenabstand, da die angeschlossene Spannungsquelle den Ausgleich vornimmt.
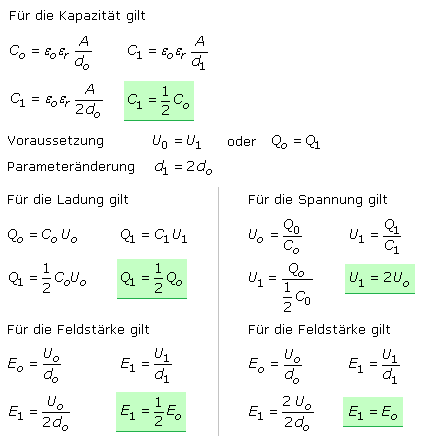
Kann sich die Ladungsmenge bei abgetrennter Spannungsquelle nicht ändern, dann verhält sich die Spannung am Kondensator proportional zum Plattenabstand und die elektrische Feldstärke bleibt gleich.
Eigenschaften des Dielektrikums
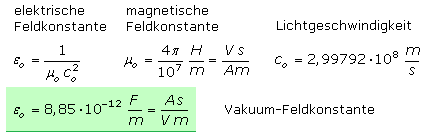
Die Elektroden des Kondensators sind gegeneinander isoliert. Eine materialfreie Isolierung ist das Vakuum, das vom elektrischen Feld durchdrungen werden kann. Der Faktor
εo ist die Feldkonstante des elektrischen Felds im Vakuum.
Dielektrika sind Isolatorwerkstoffe und werden vom elektrischen Feld durchsetzt. Es wird zwischen unpolaren und polaren Werkstoffen unterschieden. Im elektrischen Feld werden Ladungsträger unpolarer Werkstoffe der Feldrichtung entsprechend etwas verschoben. Es bilden sich Dipolmomente aus. In polaren Werkstoffen werden die permanent vorhandenen aber statistisch ausgerichteten Dipole durch das E-Feld ausgerichtet und es werden zusätzlich Ladungsträger verschoben. Die Vorgänge werden als dielektrische Polarisation bezeichnet und sind reversibel. Ohne Einwirken des elektrischen Felds nehmen die Werkstoffe ihren Anfangszustand wieder ein.
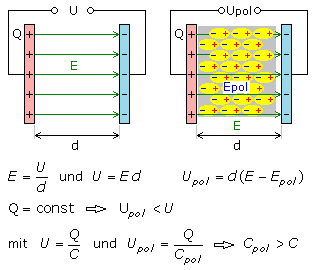
Ein Kondensator mit Luft als Dielektrikum wird mit der Spannung U geladen. Zwischen den Elektroden entsteht ein elektrisches Feld E, das umgekehrt proportional zum Elektrodenabstand und proportional zur Spannung ist. Die Spannungsquelle wird abgetrennt und die Kondensatorladung bleibt konstant.
Ein zwischen den Elektroden zusätzlich isolierendes Dielektrikum erfährt durch das elektrische Feld E eine dielektrische Polarisation. Zwischen Elektroden entsteht ein elektrisches Gegenfeld
Epol. Bleibt die Anfangsladung des Kondensators konstant, dann muss die Spannung Upol am Kondensator mit dem Dielektrikum sinken. Um wieder die Anfangsspannung U zu erreichen, muss diesem Kondensator mehr Ladung zugeführt werden. Ein Kondensator mit zusätzlichem Dielektrikum bei sonst unveränderten Parametern hat eine höhere Kapazität.
In der oben hergeleiteten Kapazitätsbeziehung Gl.(1) ist der Faktor εr die dimensionslose Permittivität. Sie charakterisiert das Isolationsmaterial zwischen den Elektroden, das als Dielektrikum bezeichnet wird. Der Wert gibt an, um welchen Faktor die Kapazität des Kondensators im Vergleich zum Vakuum (oder Luft) größer ist. In der folgenden Tabelle sind gebräuchliche Dielektrika und ihre Permittivitäten aufgeführt:
Unpolare Dielektrika
In unpolaren Werkstoffen ist die Ladungsverteilung in den Molekülstrukturen symmetrisch. Es bilden sich keine permanenten Dipole, die ein äußeres elektrisches Feld beeinflussen.
Wirken starke elektrische Felder ein, kann es zur Verschiebungspolarisation kommen, die der Feldrichtung bis in sehr hohe Frequenzen proportional folgt. Die Permittivität dieser Dielektrika,
zu denen Polyethylen (PE), Polystyrol (PS) und Polytetrafluorethylen (PTFE), Teflon gehören, ist mit <5 niedrig.
Polare Dielektrika
Die Moleküle polarer Dielektrika haben Ladungsschwerpunkte und bilden permanente Dipole. Sie sind im Molekülverband weitgehend statistisch ungeordnet ausgerichtet. Äußere elektrische Feldkräfte erzeugen eine zur Feldstärke proportionale Orientierungspolarisation. Die Orientierungsarbeit wird vom elektrischen Feld aufgebracht. Die molekularen Dipole folgen dem Feld nicht trägheitslos.
Sie werden von den molekularen Bindungskräften, der Dichte und der Temperatur in ihrer Ausrichtung beeinflusst. Nach Ablauf der Relaxationszeit, die zur Ausrichtung aller Dipole notwendig ist,
erreicht das Dielektrikum seine maximale Permittivität. Mit zunehmender Feldfrequenz können sich die Dipole immer weniger umorientieren, sodass die Permittivität und die Kapazität abnehmen.
Polare Dielektrika sind zum Beispiel Papier, Bakelit, ein Isolator aus Phenolharzen und Zellstoffpartikeln, Polyvinylchlorid (PVC), Polyester (PET, PBT), Mylar (BoPET) und Polycarbonat (PC) eine Veresterung mit Kohlensäure. In Tabellenwerken werden die Permittivitäten meist für niedrige Frequenzen angegeben und sind mit εr <10 nicht sehr hoch.
Ferroelektrika
Ferroelektrika sind polare Dielektrika mit permanentem Dipolcharakter. Sie enthalten kein Eisen, nur die Namensgebung orientierte sich an den Eigenschaften ferromagnetischer Werkstoffe.
Die Molekulardipole sind in kleineren Bereichen (Domänen) parallel zueinander ausgerichtet. Entlang der Bereichsgrenzen ist eine Ausrichtung durch anliegende elektrische Felder leicht möglich.
Es lineare Abhängigkeit der Permittivitätswerte von der Frequenz, der Feldstärke und der Temperatur gibt es nicht.
Bei einer bestimmten Temperatur, der Curie-Temperatur, bricht die Dipolausrichtung zusammen. Nach dem Abkühlen reorganisieren sich die Dipole und stellen den permanenten Dipolcharakter des Werkstoffs wieder her. Basiswerkstoffe sind Barium- und Strontiumtitanat, die zu den HDK-Keramiken zählen. Diese Dielektrika erreichen sehr hohe Permittivitäten zwischen 1000 ... 20000 aus.
Kenndaten des realen Kondensators
Zur Funktionsbeschreibung von elektronischen Schaltungen genügt es meistens, nur die Haupteigenschaften der einzelnen Bauteile zu betrachten. Beim ideal angenommenen Kondensator ist es die Kapazität,
wo der Strom um genau 90° der Spannung vorauseilt. Die Praxis zeigt, dass es keine idealen Bauteile gibt. Abhängig von den aktuellen Versuchsbedingungen treten weitere meist störende Eigenschaften in Erscheinung, die jedes reale Bauteil mitbringt.
Es gibt keine idealen Bauteile. Die Idealisierung ist die der Situation angepasste vereinfachte Darstellung.
Die Anschlussleitungen eines Kondensators und ihre Kontaktstellen zu den Elektroden haben ohmsche Komponenten und bei ausreichend hohen Frequenzen wirken induktive Eigenschaften. In vielen Fällen ist diese Anschlussinduktivität vernachlässigbar. Besonders bei Folien- und Rollkondensatoren sowie allen Alu-Elektrolytkondensatoren kann sich die induktive Komponente nachteilig auf das Schaltungsverhalten auswirken. Sie ist meistens kleiner 50 nH hinzu und wird als äquivalente Serieninduktivität, ESL, Equivalent Series Inductivity (L für Induktivität) bezeichnet. Direkte Werte sind in Datenblättern selten zu finden. Da die kapazitiven und induktiven Eigenschaften zueinander entgegengesetzt wirken, ist bei hohen Frequenzen die Betriebskapazität niedriger als der angegebene Nennwert. Bei sehr hohen Frequenzen kann es zur Reihenresonanz kommen und darüber hinaus überwiegt dann die induktive Komponente.
Im Wechselstromkreis werden die Beläge des Kondensators periodisch umgeladen und die Ausrichtung vorhandener Dipole des Dielektrikums muss dem elektrischen Wechselfeld folgen. Im molekularen Bereich wird Arbeit verrichtet, sodass mit zunehmender Betriebsfrequenz die Kondensatoren messbar wärmer werden. Die freigesetzte Wärmeenergie wird einem ohmschen Wirkwiderstand zugerechnet, der mit dem Kondensator eine Reihenschaltung bildet. Gleichzeitig lassen sich damit die ohmschen Anschlusswiderstände erfassen. In Datenblättern kann er als äquivalenter Serienwiderstand, ESR,
Equivalent Series Resistance angegeben sein.
Ein aufgeladener Kondensator verliert außerhalb der Schaltung mit der Zeit seine Ladung. Das Dielektrikum ist extrem hochohmig aber kein idealer Isolator. Abhängig vom verwendeten Material verbleibt eine mehr oder weniger geringe Restleitfähigkeit, über die sich die Ladung langsam ausgleicht. Im Ersatzschaltbild ist parallel zur Kapazität der Isolationswiderstand des Dielektrikums
Riso als ohmscher Widerstand geschaltet. Mit zunehmender Frequenz verliert der Parallelstrom an Bedeutung, da in der Parallelschaltung der Blindwiderstand des Kondensators zur bestimmenden Größe wird.
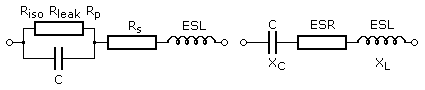
Bei Elektrolytkondensatoren steht der Parallelwiderstand Rleak als Äquivalent für den dauerhaft fließenden Reststrom. Sein Widerstandswert ist kleiner als der eigentliche
Rp, da nach Herstellerangaben konstante Restströme von einigen Microampere (μA) erlaubt sind. Dieser geringe Strom formiert das wenige Molekülschichten dicke Dielektrikum aus Aluminium- oder Tantaloxid und hält den Elko funktionsfähig. Je länger ein Elektrolytkondensator an Gleichspannung angeschlossen ist, desto größer wird dieser Widerstandswert und der anfangs einige
100 μA hohe Reststrom nimmt messbar ab.
Das Ersatzschaltbild des realen Kondensators kann als RCL-Reihenschwingkreis angesehen werden. Bei einer bestimmten Frequenz haben die beiden Blindkomponenten XC und
XESL den gleichen Wert. Im Amplituden-Frequenzdiagramm muss dann ein Minimum auftreten und der Kondensator wirkt bei dieser Frequenz nur noch wie ein ohmscher Widerstand.
Im praktischen Laborbetrieb waren messtechnisch keine Resonanzstellen zu erkennen.
Isolationswiderstand
Allgemein ist der Isolationswiderstand ein Maß für die Güte des Isoliermaterials. Beim Koaxialkabel ist es das Dielektrikum, das sich zwischen dem Leiter und dem leitenden Schirm befindet. In erster Linie bestimmen die Eigenschaften des Materials den Wert. Die genormte Messung erfolgt nach IEC 60204–1. Die Werte sind für definierte Spannungsbereiche unterschiedlich und sollten
≥1 GΩ sein. Der Isolationswiderstand für Kabel wird in der Einheit MΩ · km oder GΩ · km angegeben. Er ist von der Temperatur abhängig.
Zwischen den Metallbelägen eines Kondensators befindet sich das Dielektrikum als Isolator. Dieses Material hat einen endlichen Isolationswiderstand, da es keine idealen Isolatoren gibt.
Der Widerstandswert wird in guter Näherung nur von der Fläche und der Dicke des Dielektrikums bestimmt. Der Wert ist proportional zum Verhältnis von Dicke zur Fläche:
Riso ∝ d / A. Ebenso ist die Kapazität C des Kondensators proportional zum Verhältnis Fläche zur Dicke.
Der Isolationswiderstand entspricht dem Gleichstromwiderstand und wird bei Film- und Keramikkondensatoren für die Bezugstemperatur 20 °C fast immer in MΩ · μF angegeben.
Viele Hersteller geben den Isolationswiderstand nicht als ohmschen Wert an, sondern definieren den Isolationswert mithilfe der Zeitkonstante (tau) τ als
τ = R · C. So können Kondensatoren unterschiedlicher Kapazitätswerte einfacher miteinander verglichen werden. Mit steigender Temperatur nimmt der Isolationswert ab.
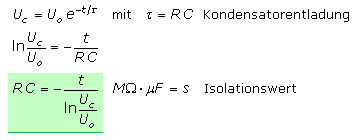
Zur experimentellen Bestimmung des Isolationswertes wird der Kondensator auf seinen Nennspannungswert aufgeladen. Er bleibt dann mit offenen Anschlüssen eine bestimmte Zeit liegen. Nach dieser Zeit wird mit einem Spannungsmessgerät mit sehr hohem Innenwiderstand (Ri > 10 MΩ) die noch im Kondensator gespeicherte Ladung als Restspannung gemessen. Aus dieser Messung können der Isolationswert und der Isolationswiderstand errechnet werden.
Im Labor wurde ein 10 μF Kondensator auf seine Nennspannung Uo = 63 V aufgeladen. Nach der Wartezeit von t = 30 min betrug die Restspannung
Uc = 30 V. Der Isolationswert errechnet sich zu τ = 2426 s, das entspricht einem Isolationswiderstand von fast
Riso = 243 MΩ.
Zur Überprüfung eines aus einem Datenblatt bekannten Isolationswerts wird der Kondensator wie oben beschrieben aufgeladen. Nach Ablauf der Zeit einer Zeitkonstante wird die Restspannung gemessen.
Liegt der Wert über 37% der Ladespannung, so wird der vom Hersteller angegebene Isolationswert eingehalten.
Der Verlustfaktor und die Güte
Im Wechselspannungsbetrieb wirken bei der Umladung der Kondensator Beläge die Feldkräfte auch auf das Dielektrikum. Die Elektronenhüllen der Festkörpermoleküle werden deformiert und sollten sie Dipolstrukturen ausbilden, werden diese der Feldrichtung entsprechend umorientiert. Die Verschiebearbeit im Dielektrikum wird zum Teil in Wärme umgewandelt. Mit steigender Frequenz nimmt die Wärmeentwicklung solange zu, bis die Umorientierung der Molekulardipole der Erregerfrequenz nicht mehr folgen kann.
Die dem Kondensator zugeführte Arbeit teilt sich in zwei Komponenten auf. Ein Teil erzeugt das E-Feld der ideal angenommenen Kapazität. Der zweite Teil wird in Wärme umgesetzt und einem zu C parallel liegenden ohmschen Widerstand zugerechnet. Er ist mit einem Ohmmeter nicht messbar und auch nicht identisch mit dem Isolationswiderstand des Dielektrikums.
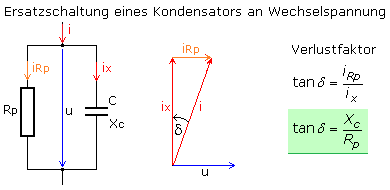
Bei der Aufstellung des Zeigerdiagramms ist für die Parallelschaltung die anliegende Spannung der Bezug. Mit zunehmender Frequenz nehmen der Blindleitwert des Kondensators und der Blindstrom
ix zu. Solange die Umorientierung im Dielektrikum dem anliegenden Wechselfeld folgen kann, wird auch mehr Wärmeenergie erzeugt. Sie wird dem äquivalenten Parallelwiderstand zugeordnet, dessen Wert abnimmt, wobei der Wirkstromanteil durch den Widerstand zunimmt. Bei vergleichbar linearer Änderung beider Größen sollte der Verlustfaktor frequenzunabhängig sein. In der Praxis zeigen sich für die unterschiedlichen Dielektrika recht unterschiedliche Frequenzabhängigkeiten des Verlustfaktors.
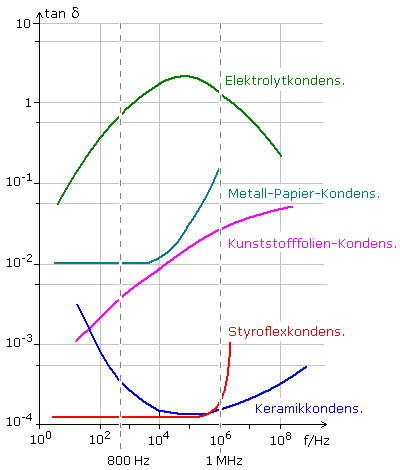
Das folgende Diagramm gibt darüber Auskunft (Quelle: Betz, Huber, Grundkenntnisse Elektrotechnik – Energietechnik / Nachrichtentechnik 1980). Vom Hersteller wird der Verlustfaktor für eine bestimmte Frequenz angegeben. Die Angaben erfolgen für 800 Hz oder 1 MHz. Mit steigender Frequenz können die Molekularstrukturen dem einwirkenden Wechselfeld nicht mehr so schnell folgen.
Die verzögerte Umorientierung wirkt sich additiv auf den Verlustwinkel aus.
Der zum Kondensator fließende Strom ist größer als der nach dem idealen Blindwiderstand berechnete Strom. Schaltungstechnisch ist das durch die Parallelschaltung eines ohmschen Widerstands möglich.
Im Wechselstromkreis kann ein Parallelwiderstand reversibel in seinen äquivalenten Reihenwiderstand umgerechnet werden. Der sehr große Wert eines Parallelwiderstands hat als Serienwiderstand dann einen sehr kleinen Wert.
Ebenfalls erfasst werden sollen auch die ohmschen Verluste der Kontaktierungen und Bauteilanschlüsse, die mit dem Kondensator eine Reihenschaltung bilden. Alle auftretenden ohmschen Verluste werden einem Ersatzreihenwiderstand ESR (equivalent series resistor) zugeordnet. Bei Rollkondensatoren kommt noch eine induktive Komponente hinzu, die auch den induktiven Anteil der Anschlussdrähte bei sehr hohen Frequenzen berücksichtigt. Beide Werte zusammen ergeben den ESL-Blindwiderstand.
Der Verlustfaktor d oder DF (dissipation factor) ist das Verhältnis des ESR zum kapazitiven Blindwiderstand. Er ist von der Frequenz abhängig und entspricht dem Tangens des Verlustwinkels δ. Er wird oft in Prozent angegeben und errechnet sich nach der Formel:
DF = RESR · ω · C · 100 %. Ebenso finden sich Wertangaben in der Form
tanδ·exp(−4) mit der Bedeutung tanδ = Wert·exp(−4).
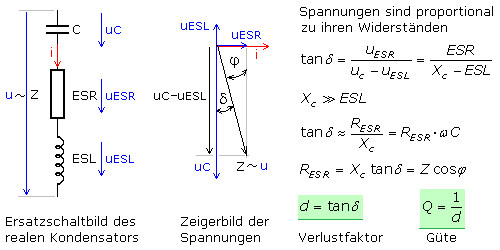
Die Bestimmung des Verlustfaktors d geht, wie es derzeit üblich ist, von der Reihenersatzschaltung des realen Kondensators aus. Mit dem Strom als Bezugsgröße einer Reihenschaltung kann das Zeigerdiagramm der Spannungen erstellt werden. Der Tangens des Verlustwinkels δ ist das Verhältnis des Serienwiderstands zum Differenzwert beider Blindwiderstände XC
und ESL. Der Gütefaktor Q ist das Verhältnis der im Kondensator gespeicherten Energie zu den Energieverlusten und ist der Kehrwert des Verlustfaktors d.
Je kleiner der ESR-Wert ist, desto kleiner werden der Verlustwinkel und damit der Verlustfaktor. Die Phasenverschiebung von Spannung und Strom durch den Kondensator geht dann gegen
φ = 90°. Die meisten Hersteller geben in den Datenblättern den Verlustfaktor tan(δ) an. ESR-Werte sind seltener zu finden, können aber aus den frequenzabhängigen Verlustfaktoren und der Kapazität berechnet werden. Dazu festgelegte Messfrequenzen sind 1 kHz, 10 kHz und 100 kHz. Die sehr kleinen und daher vernachlässigbaren ESL-Werte werden fast nie angegeben.
MSK-Folienkondensatoren haben für tan(δ) mit (0,01 ... 0,03)·exp(−3) sehr kleine Verlustfaktoren.
Bei Al-Elektrolytkondensatoren liegen die Werte bei 0,2 ... 0,07. deutlich höher. Die Messfrequenz beträgt 120 Hz.
Bei Tantal Elektrolytkondensatoren sind die Verlustfaktoren mit 0,1 ... 0,04 etwas kleiner. Oft sind es keine Folien- sondern Sinterkondensatoren.
Für Elektrolytkondensatoren wird ein maximal erlaubter DC-Leakstrom (Reststrom) nach einer Betriebszeit von 2 oder 5 Minuten angegeben. Viele Hersteller benutzen eigene Formeln zur Berechnung des Leakstroms, die sich in einem Faktor mit der Dimension A/(V·μF) und einem zusätzlichen μA-Stromwert unterscheiden. Der Reststrom errechnet sich aus der Kapazität in μF, der DC-Spannung in V und einem Faktor zwischen 0,03 ... 0,001.
Für Al-Elektrolytkondensatoren: Ileak ≤ 0,01·C·U in A oder 5 μA.
Für Tantal Elektrolytkondensatoren: Ileak < 0,005·C·U + 0,5 μA.
Nach normiertem Standard soll der Reststrom nach 5 Minuten Messdauer auf den Wert Ileak < 4 μA + 0,3·(U·C)·0,7 abgesunken sein.
Die Verlustleistung eines Kondensators
Im Wechselspannungs- und Impulsbetrieb werden Kondensatoren spürbar warm. Die Verlustleistung, die im Dielektrikum eines Kondensators umgesetzt wird, kann bei Kenntnis des Verlustfaktors berechnet werden:

Eine Beispielrechnung zeigt, dass die auftretende Verlustleistung nicht vernachlässigbar klein ist. Ein Metall-Papierkondensator mit C = 1 μF wird in einer Schaltung mit 100 V und der Frequenz f = 5 kHz betrieben. Der Verlustfaktor kann aus dem Diagramm oben zu tan(δ) = 0,01 entnommen werden. Die Verlustleistung errechnet sich dann zu
Pv = 3 W.
Für hohe Frequenzen sollten Kondensatoren mit kleinem Verlustfaktor verwendet werden.
Kondensatoren mit großem Verlustfaktor sollten nur mit niedriger Wechselspannung betrieben werden.
Das Temperaturverhalten der Kapazität
Das Dielektrikum bewirkt eine Temperaturabhängigkeit der Kapazitätswerte. Der Nennwert der Kapazität gilt für δ = 20 °C. Der Hersteller gibt den Temperaturkoeffizienten
TKC in 1/°C für einen bestimmten Temperaturbereich an. Der TK-Wert kann positiv oder negativ sein und steht für eine auf den Nennwert bezogene Kapazitätsänderung bei einer Änderung der Temperatur um 1 °C.
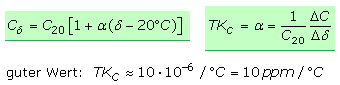
Abweichend von dieser Gleichung haben in den HDK-Keramikkondensatoren Dielektrika mit besonders hoher Permittivität nichtlineare Temperaturabhängigkeiten mit einem Maximum bei der Curie-Temperatur.
In den meisten praktischen Anwendungen ist der TK-Wert von untergeordneter Bedeutung. Wichtig ist seine Beachtung in speziellen Oszillatorschaltungen und Geräten zu Eichzwecken.